题目内容
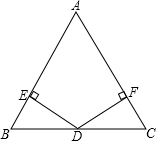 如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.(1)求证:DE=DF;
(2)若∠A=90°,图中与DE相等的有哪些线段?(不说明理由)
考点:等腰三角形的性质,等腰直角三角形
专题:
分析:(1)首先连接AD,由AB=AC,D是BC的中点,根据三线合一的性质,可得∠EAD=∠FAD,再根据角平分线的性质即可证得DE=DF;
(2)若∠BAC=90°,则∠EAD=∠FAD=∠B=∠C=45°,△ADE、△ADF、△BDE、△CDF都是等腰直角三角形,所以图中与DE相等的有线段AE、AF、BE、CF.
(2)若∠BAC=90°,则∠EAD=∠FAD=∠B=∠C=45°,△ADE、△ADF、△BDE、△CDF都是等腰直角三角形,所以图中与DE相等的有线段AE、AF、BE、CF.
解答: 解:(1)如图,连接AD.
解:(1)如图,连接AD.
∵AB=AC,D是BC的中点,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,垂足分别为E、F,
∴DE=DF;
(2)若∠BAC=90°,图中与DE相等的有线段AE、AF、BE、CF.
 解:(1)如图,连接AD.
解:(1)如图,连接AD.∵AB=AC,D是BC的中点,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,垂足分别为E、F,
∴DE=DF;
(2)若∠BAC=90°,图中与DE相等的有线段AE、AF、BE、CF.
点评:本题考查了等腰三角形的性质、角平分线的性质、等腰直角三角形的判定与性质,难度适中.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,边长为1的正方形ABCD绕点A逆时针旋转45°到正方形AB′C′D′,图中重合部分的面积为
如图,边长为1的正方形ABCD绕点A逆时针旋转45°到正方形AB′C′D′,图中重合部分的面积为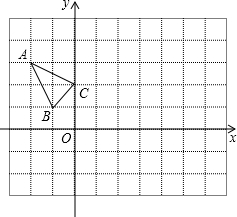 △ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).
△ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2). 阅读材料:
阅读材料: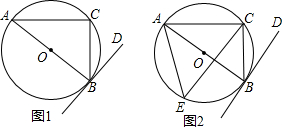

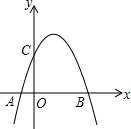 如图,抛物线y=-
如图,抛物线y=-