题目内容
 如图,以矩形ABCD的顶点C为圆心作⊙C,⊙C分别交AB、CD于P、Q两点,当CB=2,CQ=4,CD=7时,阴影部分的面积为
如图,以矩形ABCD的顶点C为圆心作⊙C,⊙C分别交AB、CD于P、Q两点,当CB=2,CQ=4,CD=7时,阴影部分的面积为考点:扇形面积的计算,含30度角的直角三角形,矩形的性质
专题:
分析:连接PC,求出扇形CPQ的面积,再求出三角形PBC的面积,矩形面积减去扇形和三角形面积即可.
解答: 解:连接CP.
解:连接CP.
∵CQ=4,
∴CP=4,
∴PB=
=
=2
,
∴tan∠PCB=
=
=
,
∴∠PCB=60°,
∴∠PCB=90°-60°=30°,
∴S扇形CPQ=
=
,
S△CPB=
×2×2
=2
,
∴S阴影=7×2-2
-
π=14-2
-
π.
故答案为14-2
-
π.
 解:连接CP.
解:连接CP.∵CQ=4,
∴CP=4,
∴PB=
| CP2-CB2 |
| 42-22 |
| 3 |
∴tan∠PCB=
| PB |
| BC |
2
| ||
| 2 |
| 3 |
∴∠PCB=60°,
∴∠PCB=90°-60°=30°,
∴S扇形CPQ=
| 30π42 |
| 360 |
| 4π |
| 3 |
S△CPB=
| 1 |
| 2 |
| 3 |
| 3 |
∴S阴影=7×2-2
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
故答案为14-2
| 3 |
| 4 |
| 3 |
点评:本题考查了扇形面积的计算、含30°角的直角三角形和矩形的面积及勾股定理,有一定的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
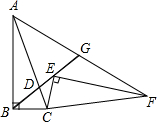 如图,在Rt△ABC中,∠B=90°,sin∠BAC=
如图,在Rt△ABC中,∠B=90°,sin∠BAC=| 1 |
| 3 |
A、
| ||||
B、3
| ||||
C、3
| ||||
D、
|
4的算术平方根是( )
| A、2 |
| B、-2 |
| C、±2 |
| D、a2+a2=a4 |
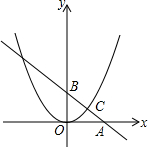 如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是
如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是 如图,边长为1的正方形ABCD绕点A逆时针旋转45°到正方形AB′C′D′,图中重合部分的面积为
如图,边长为1的正方形ABCD绕点A逆时针旋转45°到正方形AB′C′D′,图中重合部分的面积为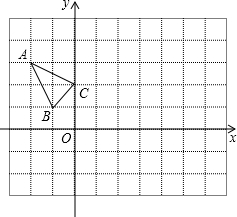 △ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).
△ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).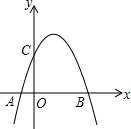 如图,抛物线y=-
如图,抛物线y=-