题目内容
在平面直角坐标系中,O为坐标原点,一次函数y=ax+b的图象与二次函数y=ax2+bx的图象交于点A、B.其中a、b均为非零实数.
(1)当a=b=1时,求AB的长;
(2)当a>0时,请用含a、b的代数式表示△AOB的面积;
(3)当点A的横坐标小于点B的横坐标时,过点B作x轴的垂线,垂足为B′.若二次函数y=ax2+bx的图象的顶点在反比例函数y=
的图象上,请用含a的代数式表示△BB′A的面积.
(1)当a=b=1时,求AB的长;
(2)当a>0时,请用含a、b的代数式表示△AOB的面积;
(3)当点A的横坐标小于点B的横坐标时,过点B作x轴的垂线,垂足为B′.若二次函数y=ax2+bx的图象的顶点在反比例函数y=
| a |
| x |
考点:二次函数综合题
专题:
分析:(1)将a=b=1代入一次函数和二次函数的解析式,再由解析式建立方程组就可以求出A、B坐标,由两点间的距离公式就可以求出AB的值;
(2)由函数的解析式就可以表示出A、B的坐标,再根据三角形的面积公式分类讨论就可以表示出△AOB的面积;
(3)由y=ax2+bx就可以求出抛物线的顶点坐标,进而就可以求出b=2a,表示出A、B的坐标,而求出B′的坐标,从而求出AB′和BB′的值,分类讨论由三角形的面积公式就可以求出结论.
(2)由函数的解析式就可以表示出A、B的坐标,再根据三角形的面积公式分类讨论就可以表示出△AOB的面积;
(3)由y=ax2+bx就可以求出抛物线的顶点坐标,进而就可以求出b=2a,表示出A、B的坐标,而求出B′的坐标,从而求出AB′和BB′的值,分类讨论由三角形的面积公式就可以求出结论.
解答:解:(1)当a=b=1时,
∴一次函数为y=x+1,二次函数为y=x2+x.
∴
,
∴
,
,
∴点A,B的坐标为(1,2)或(-1,0).
∴AB=
=2
.
答:AB的长为2
;
(2)由ax+b=ax2+bx得ax2+(b-a)x-b=0,解得:x1=-
,x2=1.
不妨设A(-
,0),B(1,a+b).
当b>0时,S△AOB=
×
(a+b)=
;
当b=0时,△AOB不存在.
当-a<b<0时,S△AOB=
×(-
)(a+b)=-
;
当b=-a时,△AOB不存在.
当b<-a时,S△AOB=
×(-
)(-a-b)=
;
(3)∵y=ax2+bx,
∴y=a(x+
)2-
,
∴抛物线的顶点坐标为:(-
,-
).
∵抛物线的顶点在双曲线y=
上,
∴-
=-
,
∴-b3=-8a3.
∴b=2a.
∴A(-2,0),B(1,3a).
∵BB′⊥x轴于点B′,
∴B′(1,0),
∴AB′=3,BB′=|3a|.
∴S△ABB′=
AB′•BB′.
当a>0时,S△ABB′=
AB′•BB′=
.
当a<0时,S△ABB′=
AB′•BB′=-
.
∴一次函数为y=x+1,二次函数为y=x2+x.
∴
|
∴
|
|
∴点A,B的坐标为(1,2)或(-1,0).
∴AB=
| 22+22 |
| 2 |
答:AB的长为2
| 2 |
(2)由ax+b=ax2+bx得ax2+(b-a)x-b=0,解得:x1=-
| b |
| a |
不妨设A(-
| b |
| a |
当b>0时,S△AOB=
| 1 |
| 2 |
| b |
| a |
| b(a+b) |
| 2a |
当b=0时,△AOB不存在.
当-a<b<0时,S△AOB=
| 1 |
| 2 |
| b |
| a |
| b(a+b) |
| 2a |
当b=-a时,△AOB不存在.
当b<-a时,S△AOB=
| 1 |
| 2 |
| b |
| a |
| b(a+b) |
| 2a |
(3)∵y=ax2+bx,
∴y=a(x+
| b |
| 2a |
| b2 |
| 4a |
∴抛物线的顶点坐标为:(-
| b |
| 2a |
| b2 |
| 4a |
∵抛物线的顶点在双曲线y=
| a |
| x |
∴-
| b2 |
| 4a |
| a | ||
|
∴-b3=-8a3.
∴b=2a.
∴A(-2,0),B(1,3a).
∵BB′⊥x轴于点B′,
∴B′(1,0),
∴AB′=3,BB′=|3a|.
∴S△ABB′=
| 1 |
| 2 |
当a>0时,S△ABB′=
| 1 |
| 2 |
| 9a |
| 2 |
当a<0时,S△ABB′=
| 1 |
| 2 |
| 9a |
| 2 |
点评:本题考查了二元二次方程组的解法的运用,二次函数的顶点式的运用,两点间的距离公式的运用,三角形的面积公式的运用,分类讨论思想的运用,解答时运用二次函数的解析式与一次函数的解析式建立方程组求交点坐标是关键.

练习册系列答案
相关题目
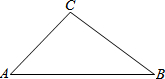 如图,在△ABC中,∠A=45°,∠B=30°,AC=
如图,在△ABC中,∠A=45°,∠B=30°,AC=| 2 |
| A、3 | ||
B、2
| ||
C、2+
| ||
D、1+
|
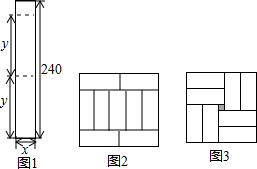 某公司欲将数张长240cm宽xcm的矩形板材裁成长ycm宽xcm的小矩形用于制作装饰图案,如图1是裁法的示意图.矩形板材沿虚线裁成若干个小块.若裁出的小矩形能组成图2的图案,此裁法记为方案一;若裁出的小矩形能组成图3的图象(中间是边长为10cm的其他材质小正方形,此裁法记为方案二.
某公司欲将数张长240cm宽xcm的矩形板材裁成长ycm宽xcm的小矩形用于制作装饰图案,如图1是裁法的示意图.矩形板材沿虚线裁成若干个小块.若裁出的小矩形能组成图2的图案,此裁法记为方案一;若裁出的小矩形能组成图3的图象(中间是边长为10cm的其他材质小正方形,此裁法记为方案二.
 已知:如图,△ABC是一块等腰三角形的余料,王师傅要在该余料上面截出一块面积最大的半圆形桌面,请你用尺规作图的方法画出这块半圆形桌面.(在题目的原图中完成作图)
已知:如图,△ABC是一块等腰三角形的余料,王师傅要在该余料上面截出一块面积最大的半圆形桌面,请你用尺规作图的方法画出这块半圆形桌面.(在题目的原图中完成作图) 如图,在平面直角坐标系中,反比例函数
如图,在平面直角坐标系中,反比例函数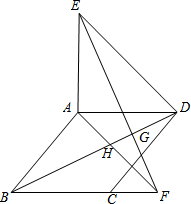 已知:如图,四边形ABCD是平行四边形,分别以AB、AD为腰作等腰三角形△ABF和等腰三角形△ADE,且顶角∠BAF=∠DAE,联结BD、EF相交于点G,BD与AF相交于点H.
已知:如图,四边形ABCD是平行四边形,分别以AB、AD为腰作等腰三角形△ABF和等腰三角形△ADE,且顶角∠BAF=∠DAE,联结BD、EF相交于点G,BD与AF相交于点H.