Question

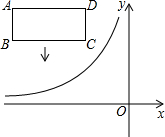如图，在平面直角坐标系中，反比例函数y=

k

x

的图象和矩形ABCD在第二象限，AD平行于x轴，且AB=2，AD=4，点C的坐标为（-2，4）．
（1）直接写出A、B、D三点的坐标；
（2）若将矩形只向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，求反比例函数的解析式和此时直线AC的解析式y=mx+n．并直接写出满足

k

x

＜mx+n的x取值范围．

Answer 1

考点：反比例函数与一次函数的交点问题,平移的性质

专题：

分析： 先根据矩形的对边平行且相等的性质得到A、B、D三点的坐标，再从矩形的平移过程发现只有B、D两点能同时在双曲线上（这是种合情推理，不必证明），把B、D两点坐标代入y=

k

x

中，再求得A、C的点的坐标代入y=mx+n中．得到关于m、n、k的方程组从而求得相应相应的值．

解答：解：（1）A（-6，6），B（-6，4），D（-2，6）．
（2）如图，矩形ABCD向下平移后得到矩形，
设平移距离为a，则B′（-6，4-a），D′（-2，6-a）∵点B′，点D′在y=

k

x

的图象上，
∴-6（4-a）=-2（6-a），
解得a=3，
∴点A′（-6，3），B′（-6，1），C′（-2，1），D′（-2，3），
将点B′（-6，1）代入y=

k

x

得：k=-6，
∴反比例函数的解析式为y=-

6

x

．
将A′（-6，3），C′（-2，1）点代入y=mx+n中得：

3=-6m+n 1=-2m+n

，
解得：

m=- 1 2 n=0

，
所以它的解析式为：y=-

1

2

x
满足

k

x

＜mx+n的x取值范围即是-

6

x

＜-

1

2

x的取值范围，即：x＜-2

3

．
 

点评：本题以矩形为背景考查用待定系数法求反比例函数的解析式．把线段的长转化为点的坐标，在求k的值的时候，由于k的值等于点的横坐标与纵坐标之积，所以直接可得方程求出相应坐标后，再由坐标求k，在本题中要注意相关数形结合思想的正确运用．