Question

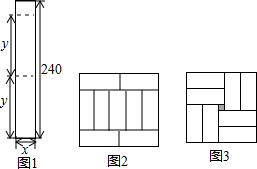某公司欲将数张长240cm宽xcm的矩形板材裁成长ycm宽xcm的小矩形用于制作装饰图案，如图1是裁法的示意图．矩形板材沿虚线裁成若干个小块．若裁出的小矩形能组成图2的图案，此裁法记为方案一；若裁出的小矩形能组成图3的图象（中间是边长为10cm的其他材质小正方形，此裁法记为方案二．
（1）根据题意完成下面表格：

	x	…	10	30	50	…
方案一	y	…	25		125	…
方案二	y	…	30	70		…

（2）方案一y与x满足的函数关系是

 

；方案二y与x满足的函数关系是

 

；
（3）若每张板材只能裁出3块可用的小矩形，那么y的取值范围是

 

；
（4）当x=在

 

范围内，不论按哪种方案裁剪，每张板材都只能裁出4块可用的小矩形；在此范围内从节约板材的角度分析，应选择方案一还是方案二．

Answer 1

考点：一次函数的应用,二元一次方程组的应用

专题：

分析：（1）利用已知数据变化规律，即可填空得出即可；
（2）利用待定系数法求一次函数解析式得出即可；
（3）利用已知矩形的长以及只能裁出3块可用的小矩形，进而得出y的取值范围；
（4）利用已知矩形的长以及只能裁出4块可用的小矩形，进而得出y的取值范围；再将两函数解析式联立求出其交点坐标即可．

解答：解：（1）填表如下：

	x	…	10	30	50	…
方案一	y	…	25	75	125	…
方案二	y	…	30	70	110	…

（2）方案一：设解析式为：y=kx，将（10，25）代入得出：25=10k，解得：k=2.5，
故解析式为：y=2.5x，
方案二：设解析式为：y=ax+b，将（10，30），（30，70）代入得出：

10k+b=30 30k+b=70

，
解得：

k=2 b=10

∴解析式为：y=2x+10；
故答案为：y=2.5x；y=2x+10；

（3）∵每张板材只能裁出3块可用的小矩形，矩形的长为240cm，
∴y的取值范围是：60＜y≤80；
故答案为：60＜y≤80；

（4）∵每张板材都只能裁出4块可用的小矩形，
∴y的取值范围是：48＜y≤60；
∴19.2＜x≤24，
解方程组 

y=2.5x y=2x+10

，
得：

x=20 y=50

，
∴当x=20时，两种方案板材利用面积相同，由函数图象性质可知，
当 19.2＜x＜20时，方案一更节约；
当 20＜x≤24时，方案二更节约．
故答案为：19.2＜x≤24．

点评：此题主要考查了一次函数的应用以及不等式解法和待定系数法求一次函数解析式等知识，利用已知数据得出y与x的函数关系式是解题关键．