Question

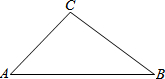如图，在△ABC中，∠A=45°，∠B=30°，AC=

2

，则AB的长为（　　）

• A、3
• B、2

  3

• C、2+

  2

• D、1+

  3

Answer 1

考点：解直角三角形

专题：计算题

分析：作CD⊥AB于D，在Rt△ACD中，由于∠A=45°，AC=

2

，根据等腰直角三角形的性质得AD=CD=

2

2

AC=1，在Rt△BDC中，由于CD=1，∠B=30°，根据含30度的直角三角形三边的关系得BD=

3

CD=

3

，所以AB=AD+BD=1+

3

．

解答：解：作CD⊥AB于D，如图，
在Rt△ACD中，∠A=45°，AC=

2

，
∴AD=CD=

2

2

AC=

2

2

×

2

=1，
在Rt△BDC中，CD=1，∠B=30°，
∴BD=

3

CD=

3

，
∴AB=AD+BD=1+

3

．
故选D．

点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．