Question

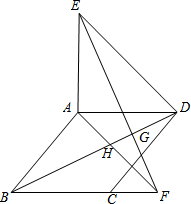已知：如图，四边形ABCD是平行四边形，分别以AB、AD为腰作等腰三角形△ABF和等腰三角形△ADE，且顶角∠BAF=∠DAE，联结BD、EF相交于点G，BD与AF相交于点H．
（1）求证：BD=EF；
（2）当线段FG、GH和GB满足怎样的数量关系时，四边形ABCD是菱形，并加以证明．

Answer 1

考点：相似三角形的判定与性质,全等三角形的判定与性质,平行四边形的性质,菱形的判定

专题：

分析：（1）求出∠BAD=∠FAE，根据全等三角形的判定推出△BAD≌△FAE，即可得出答案；
（2）根据相似三角形的判定推出△GHF∽△GFB，推出∠EFA=∠FBD，求出AB=AD，根据菱形的判定推出即可．

解答：（1）证明：∵∠BAF=∠DAE，
∴∠BAF+∠FAD=∠DAE+∠FAD，
即∠BAD=∠FAE，
在△BAD和△FAE中，

AB=AF ∠BAD=∠EAF AD=AE

∴△BAD≌△FAE（SAS），
∴BD=EF．

（2）当线段满足FG²=GH×GB时，四边形ABCD是菱形，
证明：∵FG²=GH×GB，
∴

FG

BG

=

GH

FG

，
 又∵∠BGF=∠FGB，
∴△GHF∽△GFB，
∴∠EFA=∠FBD，
∵△BAD≌△FAE，
∴∠EFA=∠ABD，
∴∠FBD=∠ABD，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠ADB=∠FBD，
∴∠ADB=∠ABD，
∴AB=AD，
又∵四边形ABCD是平行四边形，
∴四边形ABCD是菱形．

点评：本题考查了全等三角形的性质和判定，平行四边形的性质，菱形的判定，相似三角形的性质和判定的应用，主要考查学生运用性质进行推理的能力．