Question

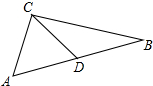如图在△ABC中，∠ACB=90°，AC=BC，∠A=∠ABC=45°，△ACD经过逆时针旋转后到达△BCE的位置．
（1）旋转中心是

 

，旋转角是

 

；
（2）除△ABC是直角三角形以外，还

 

有是直角三角形；
（3）若∠ACD=20°，求∠BDE的度数．

Answer 1

考点：旋转的性质

专题：常规题型

分析：（1）根据旋转的定义求解；
（2）根据旋转的性质得到∠DCE=90°，即△DCE为直角三角形；
（3）根据旋转的性质得∠DCE=90°，CD=CE，则△DCE为等腰直角三角形，所以∠CDE=45°，软件根据三角形外角性质得∠CDB=∠ACD+∠A，易得∠BDE=20°．

解答：解：（1）∵∠ACB=90°，AC=BC，
而△ACD逆时针旋转后到达△BCE的位置，
∴CA旋转到CB的位置，
即△ACD绕点C逆时针旋转90°后到达△BCE的位置；
（2）∵△ACD绕点C逆时针旋转90°后到达△BCE的位置，
∴∠DCE=90°，CD=CE，
∴△DCE为直角三角形；
故答案为点A，90°；△CDE；
（3）∵∠DCE=90°，CD=CE，
∴△DCE为等腰直角三角形，
∴∠CDE=45°，
∵∠CDB=∠ACD+∠A，
∴45°+∠BDE=20°+45°，
∴∠BDE=20°．

点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了等腰直角三角形的判定与性质．