题目内容
计算:
(1)(-
)-2-(-1)2006+(
)11×(-
)12;
(2)|-3|+(-1)2013×(π-3)0-(-
)-3;
(3)(y-2+x)2;
(4)(-2x+y-z)(-y-2x-z);
(5)(
a2b)•(-2ab2)2÷(-0.5a4b5);
(6)(x-y)-(-x-y)(x-y)+(x+y)2.
(1)(-
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
(2)|-3|+(-1)2013×(π-3)0-(-
| 1 |
| 2 |
(3)(y-2+x)2;
(4)(-2x+y-z)(-y-2x-z);
(5)(
| 1 |
| 4 |
(6)(x-y)-(-x-y)(x-y)+(x+y)2.
考点:整式的混合运算
专题:
分析:(1)根据负指数幂运算即可;
(2)根据绝对值、乘方、零指数幂以及负指数幂的运算性质进行计算即可;
(3)运用完全平方公式进行计算即可;
(4)运用平方差公式进行计算即可;
(5)根据单项式的乘法、除法以及幂的乘方进行计算即可;
(6)运用完全平方公式、平方差公式进行计算即可.
(2)根据绝对值、乘方、零指数幂以及负指数幂的运算性质进行计算即可;
(3)运用完全平方公式进行计算即可;
(4)运用平方差公式进行计算即可;
(5)根据单项式的乘法、除法以及幂的乘方进行计算即可;
(6)运用完全平方公式、平方差公式进行计算即可.
解答:解:(1)原式=16;
(2)原式=3+1×1+8
=3+1+8
=12;
(3)原式=(y-2)2+2x(y-2)+x2
=y2-4y+4+2xy-4x+x2;
(4)原式=[(-2x-z)+y][(-2x-z)+y]
=(-2x-z)2-y2
=(2x+z)2-y2
=4x2+4xz+z2-y2;
(5)原式=
a2b•4a2b4÷(-
a4b5)
=a4b5÷(-
a4b5)
=-2;
(6)原式=x-y-y2-x2+x2+2xy+y2.
=2xy+x-y.
(2)原式=3+1×1+8
=3+1+8
=12;
(3)原式=(y-2)2+2x(y-2)+x2
=y2-4y+4+2xy-4x+x2;
(4)原式=[(-2x-z)+y][(-2x-z)+y]
=(-2x-z)2-y2
=(2x+z)2-y2
=4x2+4xz+z2-y2;
(5)原式=
| 1 |
| 4 |
| 1 |
| 2 |
=a4b5÷(-
| 1 |
| 2 |
=-2;
(6)原式=x-y-y2-x2+x2+2xy+y2.
=2xy+x-y.
点评:本题考查了整式的混合运算,解题的关键是熟练掌握完全平方公式以及平方差公式、多项式除以单项式.

练习册系列答案
相关题目
一只不透明的口袋中原来装有1个白球、2个红球,每个球除颜色外完全相同.则下列将袋中球增减的办法中,使得将球摇匀,从中任意摸出一个球,摸到白球与摸到红球的概率不相等为( )
| A、在袋中放入1个白球 |
| B、在袋中放入1个白球、2个红球 |
| C、在袋中取出1个红球 |
| D、在袋中放入2个白球、1个红球 |
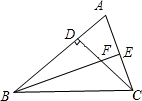 在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,并于CD相交于点F.
在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,并于CD相交于点F.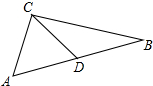 如图在△ABC中,∠ACB=90°,AC=BC,∠A=∠ABC=45°,△ACD经过逆时针旋转后到达△BCE的位置.
如图在△ABC中,∠ACB=90°,AC=BC,∠A=∠ABC=45°,△ACD经过逆时针旋转后到达△BCE的位置.