题目内容
已知关于x的一元二次方程x2-3x+k=0方程有两实根x1和x2.
(1)求实数k的取值范围;
(2)当x1和x2是一个矩形两邻边的长且矩形的对角线长为
,求k的值.
(1)求实数k的取值范围;
(2)当x1和x2是一个矩形两邻边的长且矩形的对角线长为
| 5 |
考点:根的判别式,根与系数的关系,矩形的性质
专题:判别式法
分析:(1)利用一元二次方程根的判别式即可得到关于k的不等式,从而求解;
(2)根据根与系数的关系,以及
+
=(x1+x2)2-2x1•x2=5,即9-2k=5即可求解.
(2)根据根与系数的关系,以及
| x | 2 1 |
| x | 2 2 |
解答:解:(1)∵方程有两个实数根.
∴△=(-3)2-4k≥0,即9-4k≥0.
解得k≤
;
(2)由根与系数的关系可知:x1+x2=3,x1•x2=k.
∵
+
=(x1+x2)2-2x1•x2=5,
∴9-2k=5,
∴k=2.
∴△=(-3)2-4k≥0,即9-4k≥0.
解得k≤
| 9 |
| 4 |
(2)由根与系数的关系可知:x1+x2=3,x1•x2=k.
∵
| x | 2 1 |
| x | 2 2 |
∴9-2k=5,
∴k=2.
点评:本题考查了一元二次方程根的情况与判别式△的关系和一元二次方程根与系数的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根;
(4)x1+x2=-
;
(5)x1x2=
.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根;
(4)x1+x2=-
| b |
| a |
(5)x1x2=
| c |
| a |

练习册系列答案
相关题目
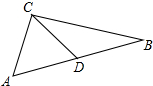 如图在△ABC中,∠ACB=90°,AC=BC,∠A=∠ABC=45°,△ACD经过逆时针旋转后到达△BCE的位置.
如图在△ABC中,∠ACB=90°,AC=BC,∠A=∠ABC=45°,△ACD经过逆时针旋转后到达△BCE的位置. 如图,8×8的正方形网格中,每个小正方形的边长为1个长度单位,点B的坐标为(1,1)点A的坐标为(3,-2)
如图,8×8的正方形网格中,每个小正方形的边长为1个长度单位,点B的坐标为(1,1)点A的坐标为(3,-2)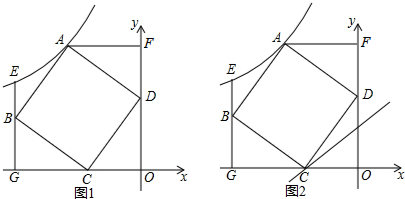
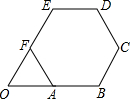 如图,正六边形ABCDEF的边长为2
如图,正六边形ABCDEF的边长为2 如图,在△ABC中,∠A=90°,AB=6,AC=8,分别以点B和C为圆心的两个等圆外切,则图中阴影部分面积为
如图,在△ABC中,∠A=90°,AB=6,AC=8,分别以点B和C为圆心的两个等圆外切,则图中阴影部分面积为