题目内容
计算:
(1)(2x2y-3xy2)-(6x2y-3xy2);
(2)(-
ax4y3)÷(-
ax2y2)•8a2y;
(3)(45a3-
a2b+3a)÷(-
a);
(4)(x-2)(x+2)-(x+1)(x-3);
(5)(1-3y)(1+3y)(1+9y2);
(6)(ab+1)2-(ab-1)2;
(7)(998)2;
(8)197×203;
(9)[(xy+2)(xy-2)-2x2y2+4],其中x=10,y=-
.
(1)(2x2y-3xy2)-(6x2y-3xy2);
(2)(-
| 3 |
| 2 |
| 6 |
| 5 |
(3)(45a3-
| 1 |
| 6 |
| 1 |
| 3 |
(4)(x-2)(x+2)-(x+1)(x-3);
(5)(1-3y)(1+3y)(1+9y2);
(6)(ab+1)2-(ab-1)2;
(7)(998)2;
(8)197×203;
(9)[(xy+2)(xy-2)-2x2y2+4],其中x=10,y=-
| 1 |
| 25 |
考点:整式的混合运算
专题:计算题
分析:(1)原式去括号合并即可得到结果;
(2)原式利用单项式乘除单项式法则计算即可得到结果;
(3)原式利用多项式除以单项式法则计算即可得到结果;
(4)原式第一项利用平方差公式化简,第二先利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(5)原式利用平方差公式计算即可得到结果;
(6)原式利用平方差公式分解,计算即可得到结果;
(7)原式变形后利用完全平方公式展开即可得到结果;
(8)原式变形后,利用平方差公式计算即可得到结果;
(9)原式利用平方差公式计算,合并得到最简结果,将x与y的值代入计算即可求出值.
(2)原式利用单项式乘除单项式法则计算即可得到结果;
(3)原式利用多项式除以单项式法则计算即可得到结果;
(4)原式第一项利用平方差公式化简,第二先利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(5)原式利用平方差公式计算即可得到结果;
(6)原式利用平方差公式分解,计算即可得到结果;
(7)原式变形后利用完全平方公式展开即可得到结果;
(8)原式变形后,利用平方差公式计算即可得到结果;
(9)原式利用平方差公式计算,合并得到最简结果,将x与y的值代入计算即可求出值.
解答:解:(1)原式=2x2y-3xy2-6x2y+3xy2=-4x2y;
(2)原式=
x2y•8a2y=10x2y2a2;
(3)原式=-135a2+
ab-9;
(4)原式=x2-4-x2+3x-x+3=2x-1;
(5)原式=(1-9y2)(1+9y2)=1-81y4;
(6)原式=(ab+1+ab-1)(ab+1-ab+1)=4ab;
(7)原式=(1000-2)2=1000000-4000+4=96004;
(8)原式=(200-3)×(200+3)=2002-32=40000-9=39991;
(9)原式=x2y2-4-2x2y2+4=-x2y2,
当x=10,y=-
时,原式=-100×
=-
.
(2)原式=
| 5 |
| 4 |
(3)原式=-135a2+
| 1 |
| 2 |
(4)原式=x2-4-x2+3x-x+3=2x-1;
(5)原式=(1-9y2)(1+9y2)=1-81y4;
(6)原式=(ab+1+ab-1)(ab+1-ab+1)=4ab;
(7)原式=(1000-2)2=1000000-4000+4=96004;
(8)原式=(200-3)×(200+3)=2002-32=40000-9=39991;
(9)原式=x2y2-4-2x2y2+4=-x2y2,
当x=10,y=-
| 1 |
| 25 |
| 1 |
| 625 |
| 4 |
| 25 |
点评:此题考查了整式的混合运算,熟练掌握运算法则及公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△ABC平移后得到△DEF,∠A=65°,∠B=35°,则∠DFG的度数是( )
如图,△ABC平移后得到△DEF,∠A=65°,∠B=35°,则∠DFG的度数是( )| A、65° | B、35° |
| C、80° | D、100° |
在平面直角坐标系中,点P在x轴下方y轴右边,且到x轴距离为3,到y轴距离为2,则点P的坐标为( )
| A、(2,-3) |
| B、(3,2) |
| C、(-2,3) |
| D、(3,-2) |
下列各式中,是分式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
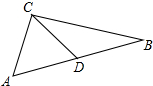 如图在△ABC中,∠ACB=90°,AC=BC,∠A=∠ABC=45°,△ACD经过逆时针旋转后到达△BCE的位置.
如图在△ABC中,∠ACB=90°,AC=BC,∠A=∠ABC=45°,△ACD经过逆时针旋转后到达△BCE的位置. 如图,8×8的正方形网格中,每个小正方形的边长为1个长度单位,点B的坐标为(1,1)点A的坐标为(3,-2)
如图,8×8的正方形网格中,每个小正方形的边长为1个长度单位,点B的坐标为(1,1)点A的坐标为(3,-2)