题目内容
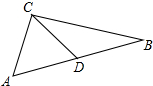
 如图,AB=AC,AB⊥AC,AD=AE,AE⊥AD,B,C,E三点在同一条直线上.
如图,AB=AC,AB⊥AC,AD=AE,AE⊥AD,B,C,E三点在同一条直线上.(1)找出图中的全等三角形,并说明理由(注意:结论中不得含有未标识的字母);
(2)探究DC与BE之间的位置关系,并说明理由;
(3)探究∠CAE与∠CDE之间的数量关系,并说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)依据SAS即可求得.
(2)由△ACD≌△ABE,可得∠ACD=∠B=45°,然后根据∠ACD+∠ACB=90°即可求得.
(3)根据∠CDE+∠AEC=45°,∠CAE+∠AEC=∠ACB=45°即可求得.
(2)由△ACD≌△ABE,可得∠ACD=∠B=45°,然后根据∠ACD+∠ACB=90°即可求得.
(3)根据∠CDE+∠AEC=45°,∠CAE+∠AEC=∠ACB=45°即可求得.
解答:(1)△ACD≌△ABE,
证明:∵AB⊥AC,AE⊥AD,
∴∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,
在△BAE与△CAD中,
∴△ACD≌△ABE(SAS),
(2)DC⊥BE,
证明:∵AB=AC,AB⊥AC,
∴∠B=∠ACB=45°,
由(1)可知△ACD≌△ABE,
∴∠ACD=∠B=45°,
∴∠BCD=∠ACD+∠ACB=90°,
∴DC⊥BE.
(3)∠CAE=∠CDE,
证明:∵AD=AE,AE⊥AD,
∴∠AED=∠ADE=45°,
∵∠CDE+∠AEC+∠AED=90°,
∴∠CDE+∠AEC=45°,
∵∠CAE+∠AEC=∠ACB=45°,
∴∠CAE=∠CDE.
证明:∵AB⊥AC,AE⊥AD,
∴∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,
在△BAE与△CAD中,
|
∴△ACD≌△ABE(SAS),
(2)DC⊥BE,
证明:∵AB=AC,AB⊥AC,
∴∠B=∠ACB=45°,
由(1)可知△ACD≌△ABE,
∴∠ACD=∠B=45°,
∴∠BCD=∠ACD+∠ACB=90°,
∴DC⊥BE.
(3)∠CAE=∠CDE,
证明:∵AD=AE,AE⊥AD,
∴∠AED=∠ADE=45°,
∵∠CDE+∠AEC+∠AED=90°,
∴∠CDE+∠AEC=45°,
∵∠CAE+∠AEC=∠ACB=45°,
∴∠CAE=∠CDE.
点评:本题考查了全等三角形的判定及性质,等腰直角三角形的性质,两直线垂直的判定等.

练习册系列答案
相关题目
在平面直角坐标系中,点P在x轴下方y轴右边,且到x轴距离为3,到y轴距离为2,则点P的坐标为( )
| A、(2,-3) |
| B、(3,2) |
| C、(-2,3) |
| D、(3,-2) |
 如图在△ABC中,∠ACB=90°,AC=BC,∠A=∠ABC=45°,△ACD经过逆时针旋转后到达△BCE的位置.
如图在△ABC中,∠ACB=90°,AC=BC,∠A=∠ABC=45°,△ACD经过逆时针旋转后到达△BCE的位置. 如图,8×8的正方形网格中,每个小正方形的边长为1个长度单位,点B的坐标为(1,1)点A的坐标为(3,-2)
如图,8×8的正方形网格中,每个小正方形的边长为1个长度单位,点B的坐标为(1,1)点A的坐标为(3,-2) 如图,正六边形ABCDEF的边长为2
如图,正六边形ABCDEF的边长为2