��Ŀ����
11�� ����ͼ��ƽ��ֱ������ϵ�У���A��B��C��������������ĸ���ϣ���ÿ��С�����εı߳�Ϊ1��
����ͼ��ƽ��ֱ������ϵ�У���A��B��C��������������ĸ���ϣ���ÿ��С�����εı߳�Ϊ1����1��д����A��B��C�����꣨-2��-1������0��2������3��-1����
��2������ABC��x�᷽������ƽ��3����λ�õ���A1B1C1������ͼ�л�����A1B1C1����ֱ��д����A1�����꣺��-5��-1����
��3����֪��ABC����x��Գ�ͼ���ǡ�A2B2C2������ͼ�л�����A2B2C����ֱ��д����B1��B2֮��ľ��룺5��
���� ��1��ֱ�Ӹ��ݸ���������ϵ�е�λ�ü��ɵó����ۣ�
��2������ͼ��ƽ�Ƶ����ʻ�����A1B1C1����ֱ��д����A1�����꼴�ɣ�
��3��������ABC����x��Գ�ͼ���ǡ�A2B2C2�����ù��ɶ������ɵó����ۣ�
���  �⣺��1����ͼ��֪��A��-2��-1����B��0��2����C��3��-1����
�⣺��1����ͼ��֪��A��-2��-1����B��0��2����C��3��-1����
�ʴ�Ϊ����-2��-1������0��2������3��-1����
��2����ͼ��A1B1C1��Ϊ����A1��-5��-1����
�ʴ�Ϊ����-5��-1����
��3����ͼ����A2B2C2��Ϊ����B1B2=$\sqrt{{3}^{2}+{4}^{2}}$=5��
�ʴ�Ϊ��5��
���� ���⿼�������ͼ-��ԳƱ任����֪��ԳƵ������ǽ�����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
1��2-2���ڣ�������
| A�� | -$\frac{1}{4}$ | B�� | -4 | C�� | 4 | D�� | $\frac{1}{4}$ |
16������A��a��-3����y���ϣ����B��a-2��a+3���ڣ�������
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
 ��ͼ����ABC�У�AB=AC��BC=3��AD��BC���ϵĸߣ���AD=4����ͼ����Ӱ���ֵ����Ϊ3��
��ͼ����ABC�У�AB=AC��BC=3��AD��BC���ϵĸߣ���AD=4����ͼ����Ӱ���ֵ����Ϊ3��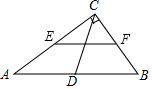 ��ͼ����ֱ��������ABC�У���ACB=90�㣬D��E��F�ֱ���AB��AC��BC���е㣬��CD=5����EF�ij�Ϊ5��
��ͼ����ֱ��������ABC�У���ACB=90�㣬D��E��F�ֱ���AB��AC��BC���е㣬��CD=5����EF�ij�Ϊ5�� ��ͼ����ƽ��ֱ������ϵxOy�У���֪A��-2��3����B��-3��1����C��-1��0����D��0��2����B1��-2��-3����������������⣺
��ͼ����ƽ��ֱ������ϵxOy�У���֪A��-2��3����B��-3��1����C��-1��0����D��0��2����B1��-2��-3����������������⣺