��Ŀ����
6����Ҫ��������и��⣮��1���ⲻ��ʽ�鲢д����������
$\left\{\begin{array}{l}{5x+2��3��x-1��}\\{1-\frac{2x+5}{3}��x-2}\end{array}\right.$
��2�������в���ʽ��
$\left\{\begin{array}{l}{\frac{1-2x}{3}-\frac{4-3x}{6}��\frac{x-2}{2}}\\{2x-7��3��x-1��}\end{array}\right.$��
���� ��1�����ÿ������ʽ�Ľ⼯�������Ҳ���ʽ��⼯�Ĺ����ҳ����ɣ�
��2�����ÿ������ʽ�Ľ⼯�������Ҳ���ʽ��⼯�Ĺ����ҳ����ɣ�
��� �⣺��1��$\left\{\begin{array}{l}{5x+2��3��x-1����}\\{1-\frac{2x+5}{3}��x-2��}\end{array}\right.$
�߽ⲻ��ʽ�ٵã�x$��-\frac{5}{2}$��
�ⲻ��ʽ�ڵã�x��$\frac{4}{5}$��
���ʽ��Ľ⼯Ϊ��-$\frac{5}{2}$��x��$\frac{4}{5}$��
������ʽ���������Ϊ��-2��-1��0��
��2��$\left\{\begin{array}{l}{\frac{1-2x}{3}-\frac{4-3x}{6}��\frac{x-2}{2}��}\\{2x-7��3��x-1����}\end{array}\right.$
�ⲻ��ʽ�ٵã�x��1��
�ⲻ��ʽ�ڵã�x��-4��
���ʽ��Ľ⼯Ϊ��-4��x��1��
���� ���⿼���˽�һԪһ�β���ʽ���飩��һԪһ�β���ʽ����������Ӧ�ã��ؼ����ܸ��ݲ���ʽ�Ľ⼯�ҳ�����ʽ��Ľ⼯��

��ϰ��ϵ�д�
�����Ŀ
18����֪$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$���Ƿ���y=kx+b�Ľ⣬��k��b��ֵ�ǣ�������
| A�� | $\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=5}\end{array}\right.$ |
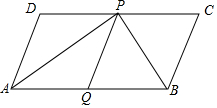 ��ͼ����?ABCD�У�AP��BP�ֱ�ƽ�֡�DAB�͡�CBA��PQ��AD����AD=5cm��AP=8cm�����ABP���������24cm2��
��ͼ����?ABCD�У�AP��BP�ֱ�ƽ�֡�DAB�͡�CBA��PQ��AD����AD=5cm��AP=8cm�����ABP���������24cm2�� ����ͼ��ƽ��ֱ������ϵ�У���A��B��C��������������ĸ���ϣ���ÿ��С�����εı߳�Ϊ1��
����ͼ��ƽ��ֱ������ϵ�У���A��B��C��������������ĸ���ϣ���ÿ��С�����εı߳�Ϊ1��