题目内容
19．计算：（1）$\sqrt{27}$-$\frac{1}{3}$$\sqrt{18}$-$\sqrt{12}$；
（2）$\sqrt{15}$÷$\sqrt{20}$×$\sqrt{1\frac{1}{3}}$．
分析 （1）先把各二次根式化为最简二次根式，然后合并即可；
（2）根据二次根式的乘除法则运算．
解答 解：（1）原式=3$\sqrt{3}$-$\sqrt{2}$-2$\sqrt{3}$
=$\sqrt{3}$-$\sqrt{2}$；
（2）原式=$\sqrt{15×\frac{1}{20}×\frac{4}{3}}$
=1．
点评 本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．
练习册系列答案
一线名师提优试卷系列答案
相关题目
10．点A（m+4，3-2m）在第二象限，则m的取值范围是（ ）
| A． | m＞-4 | B． | m＜$\frac{3}{2}$ | C． | m＜-4 | D． | -4＜m＜$\frac{3}{2}$ |
4．在一次函数y=（m-1）x+3的图象上，y随x的增大而减小，则m的取值范围是（ ）
| A． | m＞1 | B． | m＞0 | C． | m≥1 | D． | m＜1 |
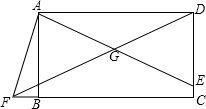如图，四边形ABCD是矩形，E是CD上一点，连接AE，取AE的中点G，连接DG并延长交CB延长线于点F，连接AF，∠AFC=3∠EAD，若DG=4，BF=1，则AB的长为$\sqrt{15}$．