题目内容
11.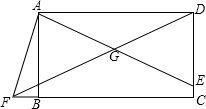 如图,四边形ABCD是矩形,E是CD上一点,连接AE,取AE的中点G,连接DG并延长交CB延长线于点F,连接AF,∠AFC=3∠EAD,若DG=4,BF=1,则AB的长为$\sqrt{15}$.
如图,四边形ABCD是矩形,E是CD上一点,连接AE,取AE的中点G,连接DG并延长交CB延长线于点F,连接AF,∠AFC=3∠EAD,若DG=4,BF=1,则AB的长为$\sqrt{15}$.
分析 先证出MG=DG,证明四边形AMED是矩形,得出AG=MG=DG=4,再证出∠AFG=∠AGF,得出AF=AG,在Rt△ABF中,根据勾股定理即可求出AB的长.
解答 解:如图所示:连接EM,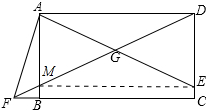 ∵G是AE的中点,
∵G是AE的中点,
∴AG=EG,
∵四边形ABCD是矩形,
∴∠DAB=∠ABC=∠ABF=90°,AB∥DC,AD∥BC,
∴$\frac{MG}{DG}=\frac{AG}{EG}$=1,
∴MG=DG,
∴四边形AMED是矩形,
∴AG=MG=DG=4,
∴∠GDA=∠EAD,
∵AD∥BC,
∴∠GDA=∠DFC,
∵∠AFC=3∠EAD,∠AGF=∠EAD+∠GDA,
∴∠AFG=∠AGF,
∴AF=AG=4,
在Rt△ABF中,AB=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$;
故答案为:$\sqrt{15}$.
点评 本题考查了矩形的性质与判定、等腰三角形的判定、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
2.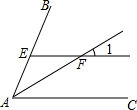 如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BAF的度数为( )
如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BAF的度数为( )
 如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BAF的度数为( )
如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BAF的度数为( )| A. | 60° | B. | 70° | C. | 35° | D. | 17.5° |
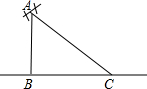 如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )
如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )