题目内容
14.已知$\left\{\begin{array}{l}{x+ay=2}\\{5x-2y=3}\end{array}\right.$的解也是二元一次方程x-y=0的一个解,则a=1.分析 联立不含a的两方程求出x与y的值,代入剩下的方程求出a的值即可.
解答 解:联立得:$\left\{\begin{array}{l}{5x-2y=3①}\\{x-y=0②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
把x=1,y=1代入x+ay=2中得:1+a=2,
解得:a=1,
故答案为:1
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
相关题目
4.为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y是x的一次函数,下表列出两套符合条件的课桌椅的高度.
(1)请确定课桌高度与椅子高度的函数关系式;
(2)现有一张高80cm的课桌和一张高为43cm的椅子,它们是否配套?为什么?
| 第一套 | 第二套 | |
| 椅子高度x(cm) | 42 | 38 |
| 课桌高度y(cm) | 74 | 70 |
(2)现有一张高80cm的课桌和一张高为43cm的椅子,它们是否配套?为什么?
2.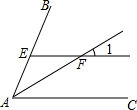 如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BAF的度数为( )
如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BAF的度数为( )
 如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BAF的度数为( )
如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BAF的度数为( )| A. | 60° | B. | 70° | C. | 35° | D. | 17.5° |
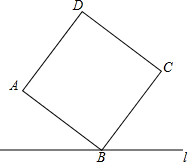 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的边长是$\sqrt{13}$.
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的边长是$\sqrt{13}$.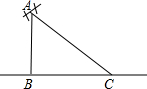 如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )
如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( ) 已知关于x的不等式3x+mx>-5的解集如图所示,则m的值为-$\frac{1}{2}$.
已知关于x的不等式3x+mx>-5的解集如图所示,则m的值为-$\frac{1}{2}$.