题目内容
8.解下列不等式(组),并把解集在数轴上表示出来.(1)$\frac{m}{3}$-$\frac{m-1}{2}$<1
(2)$\left\{\begin{array}{l}{5x+4<3(x+1)}\\{\frac{x-1}{2}≥\frac{2x-1}{5}}\end{array}\right.$.
分析 (1)首先去分母,去括号,然后移项、合并同类项,系数化成1,即可求得不等式的解集.
(2)根据不等式的性质求出不等式的解集,根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)$\frac{m}{3}$-$\frac{m-1}{2}$<1
去分母得:2m-3m+3<6,
移项得:2m-3m<6-3
合并同类项得:-m<3
则m>-3.
数轴表示为:
(2)$\left\{\begin{array}{l}{5x+4<3(x+1)①}\\{\frac{x-1}{2}≥\frac{2x-1}{5}②}\end{array}\right.$
解不等式①得:x<-$\frac{1}{2}$,
解不等式②得:x≥3,
在数轴上表示为:
∴不等式组无解.
点评 本题主要考查对不等式的性质,解一元一次不等式,解一元一次不等式组,在数轴上表示不等式组的解集等知识点的理解和掌握,能根据找不等式组解集的规律找出不等式组的解集是解此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.甲、乙两数和为21,甲数的2倍等于乙数的5倍,求甲、乙两数.设甲数为x,乙数为y,则下列方程组正确的是( )
| A. | $\left\{{\begin{array}{l}x+y=21\\ 5x=2y\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}x+y=21\\ 2x=5y\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}2x+5y=21\\ 2x=5y\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}2x+5y=21\\ 5x=2y\end{array}}\right.$ |
 如图,在△ABC中,AC的垂直平分线DE交AB于E,∠A=30°,∠ACB=70°,则∠BCE等于40°.
如图,在△ABC中,AC的垂直平分线DE交AB于E,∠A=30°,∠ACB=70°,则∠BCE等于40°.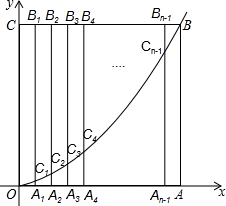 如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,当B25C25=8C25A25时,则n=75.
如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,当B25C25=8C25A25时,则n=75.