题目内容
9.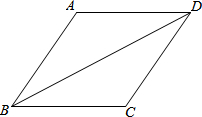 如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC,若CD=3,BD=$2\sqrt{6}$,sin∠DBC=$\frac{{\sqrt{3}}}{3}$,求对角线AC的长.
如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC,若CD=3,BD=$2\sqrt{6}$,sin∠DBC=$\frac{{\sqrt{3}}}{3}$,求对角线AC的长.
分析 过D作DE⊥BC交BC的延长线于E,得到∠E=90°,根据三角形函数的定义得到DE=2$\sqrt{2}$,推出四边形ABCD是菱形,根据菱形的性质得到AC⊥BD,AO=CO,BO=DO=$\sqrt{6}$,根据勾股定理得到结论.
解答 解:过D作DE⊥BC交BC的延长线于E,
则∠E=90°,
∵sin∠DBC=$\frac{{\sqrt{3}}}{3}$,BD=$2\sqrt{6}$,
∴DE=2$\sqrt{2}$,
∵CD=3,
∴CE=1,BE=4,
∴BC=3,
∴BC=CD,
∴∠CBD=∠CDB,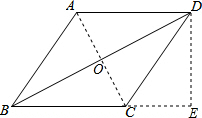
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠CDB,
∴AB∥CD,
同理AD∥BC,
∴四边形ABCD是菱形,
连接AC交BD于O,
则AC⊥BD,AO=CO,BO=DO=$\sqrt{6}$,
∴OC=$\sqrt{B{C}^{2}-B{O}^{2}}$=$\sqrt{3}$,
∴AC=2$\sqrt{3}$.
点评 本题考查了菱形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
20.下列图形中,不可以作为一个正方体的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
4.设681×2019-681×2018=a,2015×2016-2013×2018=b,$\sqrt{{{678}^2}+1358+690+678}=c$,则a,b,c的大小关系是( )
| A. | b<c<a | B. | a<c<b | C. | b<a<c | D. | c<b<a |
14.小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
| A. | 2$\sqrt{3}$cm | B. | 4$\sqrt{3}$cm | C. | 6$\sqrt{3}$cm | D. | 8$\sqrt{3}$cm |
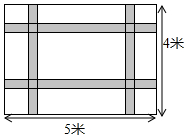 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.
如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.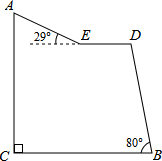 “蘑菇石”是我省著名自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1790m.如图,DE∥BC,BD=1700m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m)
“蘑菇石”是我省著名自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1790m.如图,DE∥BC,BD=1700m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m)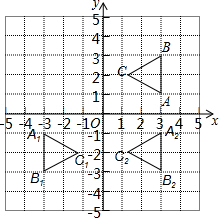 如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以原点为对称中心作△ABC的中心对称图形,得△A1B1C1,再以y轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以原点为对称中心作△ABC的中心对称图形,得△A1B1C1,再以y轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.