题目内容
8.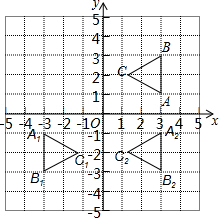 如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以原点为对称中心作△ABC的中心对称图形,得△A1B1C1,再以y轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以原点为对称中心作△ABC的中心对称图形,得△A1B1C1,再以y轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.(1)直接写出C1,C2的坐标;
(2)能否通过一次旋转,将△ABC旋转到△A1B1C1的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的角度;你若认为不能,请作出否定的回答(不必说明理由);
(3)设当△ABC的位置发生变化时,△A2B2C2,△A1B1C1与△ABC之间的对称关系始终保持不变,当△ABC向下平移多少个单位时,△ABC与△A2B2C2完全重合?并直接写出此时点C的坐标.
分析 (1)作CH⊥AB于H,如图,利用等边三角形的性质和三个顶点的坐标特征可判断∴AB∥y轴,AB=2,AH=BH=1,∠A=60°,则可写出H点坐标,接着利用含30度的直角三角形三边的关系求出CH即可得到C点坐标,然后利用关于原点和关于y轴对称的点的坐标特征可分别写出C1,C2的坐标;
(2)成中心对称的两图形都可以利用旋转完成.
(3)把△ABC向下平移到△ABC关于x轴对称时,△ABC与△A2B2C2完全重合,然后确定平移的距离.
解答 解:(1)作CH⊥AB于H,如图,
∵△ABC为等边三角形,A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),
∴AB∥y轴,AB=2,AH=BH=1,∠A=60°,
∴H(3,2),
在Rt△ACH中,CH=$\sqrt{3}$AH=$\sqrt{3}$,
∵C(3-$\sqrt{3}$,2),
∵△ABC与△A1B1C1关于原点中心对称,
∴C1(-3+$\sqrt{3}$,-2),
∵△A1B1C1与△A2B2C2关于y轴对称,
∴C2(3-$\sqrt{3}$,-2);
(2)能通过一次旋转,将△ABC旋转到△A1B1C1的位置.
把△ABC绕点O旋转180°得到△A1B1C1的位置,即旋转的角度为180°;
(3)当△ABC向下平移2个单位时,△ABC与△A2B2C2完全重合,此时点C的坐标为(3-$\sqrt{3}$,0).
点评 本题考查了几何变换综合题:熟练掌握点平移的坐标规律和关于原点和坐标轴对称的点的坐标特征;会应用等边三角形的性质计算线段的长;理解坐标与图形性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列说法正确的是( )
| A. | 单项式乘以多项式的积可能是一个多项式,也可能是单项式 | |
| B. | 单项式乘以多项式的积仍是一个单项式 | |
| C. | 单项式乘以多项式的结果的项数与原多项式的项数相同 | |
| D. | 单项式乘以多项式的结果的项数与原多项式的项数不同 |
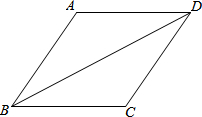 如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC,若CD=3,BD=$2\sqrt{6}$,sin∠DBC=$\frac{{\sqrt{3}}}{3}$,求对角线AC的长.
如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC,若CD=3,BD=$2\sqrt{6}$,sin∠DBC=$\frac{{\sqrt{3}}}{3}$,求对角线AC的长.