题目内容
17.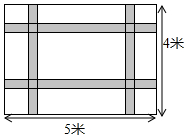 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.
如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.
分析 (1)设条纹的宽度为x米,根据等量关系:配色条纹所占面积=整个地毯面积的$\frac{17}{80}$,列出方程求解即可;
(2)根据总价=单价×数量,可分别求出地毯配色条纹和其余部分的钱数,再相加即可求解.
解答 解:(1)设条纹的宽度为x米.依题意得
2x×5+2x×4-4x2=$\frac{17}{80}$×5×4,
解得:x1=$\frac{17}{4}$(不符合,舍去),x2=$\frac{1}{4}$.
答:配色条纹宽度为$\frac{1}{4}$米.
(2)条纹造价:$\frac{17}{80}$×5×4×200=850(元)
其余部分造价:(1-$\frac{17}{80}$)×4×5×100=1575(元)
∴总造价为:850+1575=2425(元)
答:地毯的总造价是2425元.
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
相关题目
5.小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
| 商品名 | 单价(元) | 数量(个) | 金额(元) |
| 签字笔 | 3 | 2 | 6 |
| 自动铅笔 | 1.5 | ● | ● |
| 记号笔 | 4 | ● | ● |
| 软皮笔记本 | ● | 2 | 9 |
| 圆规 | 3.5 | 1 | ● |
| 合计 | 8 | 28 |
12.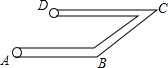 如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
 如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )| A. | AB∥BC | B. | BC∥CD | C. | AB∥DC | D. | AB与CD相交 |
2.已知压强的计算公式是P=$\frac{F}{S}$,我们知道,刀具在使用一段时间后,就好变钝,如果刀刃磨薄,刀具就会变得锋利.下列说法中,能正确解释刀具变得锋利这一现象的是( )
| A. | 当受力面积一定时,压强随压力的增大而增大 | |
| B. | 当受力面积一定时,压强随压力的增大而减小 | |
| C. | 当压力一定时,压强随受力面积的减小而减小 | |
| D. | 当压力一定时,压强随受力面积的减小而增大 |
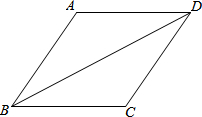 如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC,若CD=3,BD=$2\sqrt{6}$,sin∠DBC=$\frac{{\sqrt{3}}}{3}$,求对角线AC的长.
如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC,若CD=3,BD=$2\sqrt{6}$,sin∠DBC=$\frac{{\sqrt{3}}}{3}$,求对角线AC的长.