题目内容
3.下列计算中:①$\sqrt{20}$=2$\sqrt{10}$;②$\sqrt{16\frac{1}{4}}$=4$\frac{1}{2}$;③$\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$;④$\sqrt{(-2)^{2}}$=-2;⑤$\frac{\sqrt{27}-\sqrt{12}}{3}$=$\sqrt{9}$-$\sqrt{4}$=1,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据二次根据的运算,分别验证五个等式的正误,由此即可得出结论.
解答 解:①$\sqrt{20}$=2$\sqrt{5}$,故①不正确;
②$\sqrt{16\frac{1}{4}}$=$\sqrt{\frac{65}{4}}$=$\frac{\sqrt{13}}{2}$,故②不正确;
③$\sqrt{8}$-$\sqrt{2}$=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$,故③正确;
④$\sqrt{(-2)^{2}}$=$\sqrt{4}$=2,故④不正确;
⑤$\frac{\sqrt{27}-\sqrt{12}}{3}$=$\frac{3\sqrt{3}-2\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$,故⑤不正确.
综上所述:正确的结论为③.
故选A.
点评 本题考查了二次根式的加减法以及二次根式的性质与化简,熟练掌握二次根式化简的方法是解题的关键.

练习册系列答案
相关题目
14.在实数0,$\sqrt{3}$,3.14,π中,无理数的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.如图是按一定规律摆放的图案,按此规律,下列图案中与第2017个图案中的指针指向相同的图案是( )


| A. | 第1个 | B. | 第2个 | C. | 第3个 | D. | 第4个 |
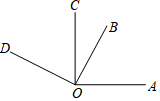 如图,CO⊥AO,DO⊥BO,∠BOC=30°,则∠AOD=150°.
如图,CO⊥AO,DO⊥BO,∠BOC=30°,则∠AOD=150°.
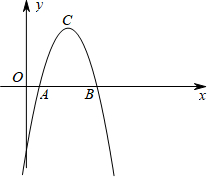 如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线l的顶点为C(3,4),抛物线l′和l关于x轴对称.
如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线l的顶点为C(3,4),抛物线l′和l关于x轴对称.