题目内容
8.如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为智慧数:如3=22-1,5=32-22,7=42-32,8=32-12,9=52-42,11=62-52…探索从1开始第20个智慧数是29.分析 根据规律可知全部智慧数从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数.归纳可得第n组的第一个数为4n(n≥2),又因为20=3×6+2,所以第20个智慧数是第7组中的第2个数,从而得到4×7+1=29.
解答 解:∵第1个智慧数3=22-12,第2个智慧数5=32-22,第3个智慧数7=42-32,
第4个智慧数8=32-12,第5个智慧数9=52-42,第6个智慧数11=62-52,
第7个智慧数12=42-22,第8个智慧数13=72-62,第9个智慧数15=42-12,
第10个智慧数16=52-32,第11个智慧数17=92-82,第12个智慧数19=102-92,
…
∴可知全部智慧数从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数.
即第n组的第一个数为4n(n≥2),
∵20=3×6+2,
∴第20个智慧数位于第7组第2个数,
∵第7组的第1个智慧数为4×7=28,
∴第7组第2个数为29,即第20个智慧数为29,
故答案为:29.
点评 本题主要考查数字的变化规律,将全部智慧数从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数是解题的关键.

练习册系列答案
相关题目
18.下列等式成立的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\sqrt{8}$=2$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
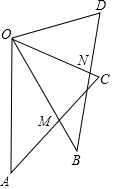 已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.
已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N. 如图,在△ABC中,∠ACB=90°,BD是△ABC的一条角平分线,DE⊥AB,垂足E,BC=6,AE=2,则AB=8.
如图,在△ABC中,∠ACB=90°,BD是△ABC的一条角平分线,DE⊥AB,垂足E,BC=6,AE=2,则AB=8. 如图,点M是直线AB上一点,∠AMC=52°48′,∠BMD=74°30′,则∠CMD=51°42′.
如图,点M是直线AB上一点,∠AMC=52°48′,∠BMD=74°30′,则∠CMD=51°42′.