题目内容
14.在实数0,$\sqrt{3}$,3.14,π中,无理数的个数有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据无理数、有理数的定义即可判定选择项.
解答 解:$\sqrt{3}$,π是无理数,
故选:C.
点评 此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,$\sqrt{6}$,0.8080080008…(每两个8之间依次多1个0)等形式.

练习册系列答案
相关题目
4.已知-4x>3,则下列不等式中,错误的是( )
| A. | -4x+1>4 | B. | -4x-3>0 | C. | x>-$\frac{3}{4}$ | D. | -$\frac{4}{3}$x>1 |
5.下列说法不正确的是( )
| A. | 0的立方根是0 | B. | 0的平方根是0 | C. | 1的立方根是±1 | D. | 4的平方根是±2 |
2.(-1)2000+(-1)2001的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
6.如图,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列计算正确的是( )
| A. | a3+a4=a7 | B. | a3•a4=a12 | C. | (a3)4=a12 | D. | a4-a3=a |
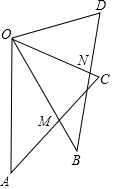 已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.
已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.