题目内容
15.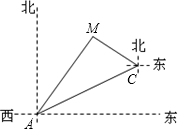 如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)
如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)
分析 过M作MN⊥AC交于N点,即MN最短,根据方向角可以证得∠AMC=90°,根据三角函数即可求得MC,进而求得AN的长.
解答 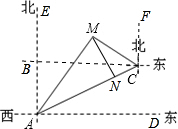 解:如图,过M作MN⊥AC交于N点,即MN最短,
解:如图,过M作MN⊥AC交于N点,即MN最短,
∵∠EAD=60°,∠CAD=30°,
∴∠CAM=30°,
∴∠AMN=60°,
又∵C处看M点为北偏西60°,
∴∠FCM=60°,
∴∠MCB=30°,
∵∠EAC=60°,
∴∠CAD=30°,
∴∠BCA=30°,
∴∠MCA=∠MCB+∠BCA=60°,
∴在Rt△AMC中,∠AMC=90°,∠MAC=30°,
∴MC=$\frac{1}{2}$AC=2000,∠CMN=30°,
∴NC=$\frac{1}{2}$MC=1000,
∵AC=4000米,
∴AN=AC-NC=4000-1000=3000(米).
答:点N到A市最短路线3000米.
点评 本题主要考查了方向角含义,正确作出高线,证明△AMC是直角三角形是解题的关键.

练习册系列答案
相关题目
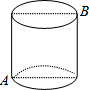 如图,己知圆柱底面周长为24cm,高为9cm,则蚂蚁在圆柱表面从A点爬到B点的最短路程是15cm.
如图,己知圆柱底面周长为24cm,高为9cm,则蚂蚁在圆柱表面从A点爬到B点的最短路程是15cm.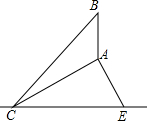 如图,CE为水平线,斜坡AC的坡度(坡比)为1:$\sqrt{3}$,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC至少准备多长?
如图,CE为水平线,斜坡AC的坡度(坡比)为1:$\sqrt{3}$,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC至少准备多长?
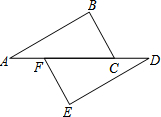 如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠A=∠D,AB=DE,BC∥EF,求证:AF=DC.
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠A=∠D,AB=DE,BC∥EF,求证:AF=DC.