题目内容
4.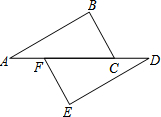 如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠A=∠D,AB=DE,BC∥EF,求证:AF=DC.
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠A=∠D,AB=DE,BC∥EF,求证:AF=DC.
分析 先由平行线的性质得出∠ACB=∠DFE,再由AAS证明△AB≌△DEF,得出对应边相等AC=DF,即可得出AF=DC.
解答 证明:∵BC∥EF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{∠A=∠D}&{\;}\\{∠ACB=∠DFE}&{\;}\\{AB=DE}&{\;}\end{array}\right.$,
∴△AB≌△DEF(AAS),
∴AC=DF,
∴AF=DC.
点评 本题考查了平行线的性质、全等三角形的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
9. 中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )
中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )
 中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )
中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )| A. | 6.75×103吨 | B. | 6.75×104吨 | C. | 6.75×105吨 | D. | 6.75×10-4吨 |
16. 如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
 如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | (a+b)(a-b)=a2-b2 | D. | a(a-b)=a2-ab |
13.计算3a•2b的结果是( )
| A. | 3ab | B. | 5ab | C. | 6a | D. | 6ab |
12. 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )| A. | 2cm2 | B. | 1cm2 | C. | 0.5cm2 | D. | 0.25cm2 |
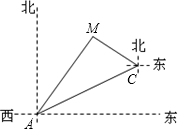 如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)
如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)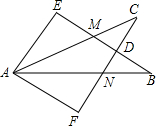 如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )
如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )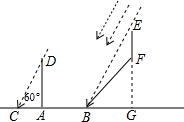 如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°
如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°