题目内容
10.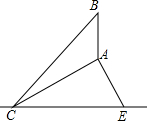 如图,CE为水平线,斜坡AC的坡度(坡比)为1:$\sqrt{3}$,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC至少准备多长?
如图,CE为水平线,斜坡AC的坡度(坡比)为1:$\sqrt{3}$,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC至少准备多长?
分析 延长BA交CE于D点,则BD⊥CE,在Rt△ACD中,得到tan∠ACD=$\frac{AD}{CD}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,求出∠ACD=30°,再根据∠ACD的正弦、余弦值,求出AD、CD的长,从而得到BD的长,然后利用勾股定理求出BC的长.
解答 解:延长BA交CE于D点,则BD⊥CE,
在Rt△ACD中,tan∠ACD=$\frac{AD}{CD}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,故∠ACD=30°,
由cos∠ACD=$\frac{CD}{AC}$知,CD=AD•cos∠ACD=10×cos30°=5$\sqrt{3}$,
由sin∠ACD=$\frac{AD}{AC}$知AD=AC•sin∠ACD=10×$\frac{1}{2}$=5,
∴BD=BA+AD=3+5=8,
在Rt△BCD中,
BC=$\sqrt{{BD}^{2}+{CD}^{2}}$=$\sqrt{(5\sqrt{3})^{2}+{8}^{2}}$=$\sqrt{75+64}$=$\sqrt{139}$,
∴$\sqrt{125}$<$\sqrt{139}$<$\sqrt{144}$
∴BC≈12米.
点评 本题考查了解直角三角形的应用--坡度坡角问题,熟悉坡度、坡角的定义及勾股定理是解题的关键.

练习册系列答案
相关题目
 如图是用吸管吸易拉罐内的饮料时的横截面,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)
如图是用吸管吸易拉罐内的饮料时的横截面,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)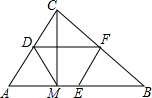 如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.
如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.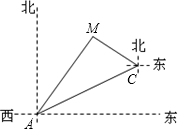 如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)
如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)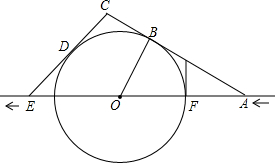 如图,某船在大海中沿航线由东向西行驶,行驶到A时,发现前方20海里的F处出现暗礁,经进一步观察发现前方以点O为圆心(点O在航线上),OF长为半径的区域内充满暗礁,该船马上改变航向,从点A沿北偏西60°方向前进,与⊙O切于点B后到达点C,接着,该船从点C沿南偏西45°方向前进,与⊙O切于点D后回到航线上点E,然后继续沿原航线行驶,请解决下列问题:暗礁区域的半径为多少海里?
如图,某船在大海中沿航线由东向西行驶,行驶到A时,发现前方20海里的F处出现暗礁,经进一步观察发现前方以点O为圆心(点O在航线上),OF长为半径的区域内充满暗礁,该船马上改变航向,从点A沿北偏西60°方向前进,与⊙O切于点B后到达点C,接着,该船从点C沿南偏西45°方向前进,与⊙O切于点D后回到航线上点E,然后继续沿原航线行驶,请解决下列问题:暗礁区域的半径为多少海里?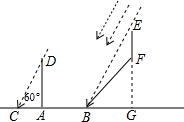 如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°
如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°