题目内容
5.已知关于x的一元二次方程x2+2x+3k-6=0有两个不相等的实数根(1)求实数k的取值范围;
(2)若k为正整数,且该方程的根都是整数,求k的值.
分析 (1)根据一元二次方程的定义和△的意义得到△=22-4×1×(3k-6)=-12k+28>0,然后解不等式即可得到k的取值范围;
(2)由(1)的范围得到k=1或k=2,然后把k=1和2代入原方程,然后解方程确定满足条件的k值即可.
解答 解:(1)∵关于x的一元二次方程x2+2x+3k-6=0有两个不相等的实数根,
△=22-4×1×(3k-6)=-12k+28>0,
∴k<$\frac{7}{3}$,
∴k的取值范围是k<$\frac{7}{3}$;
(2))∵k为正整数,
∴k=1或k=2,
当k=1时,原方程为x2+2x-3=0,解得x1=-3,x2=1,
当k=2是,原方程为x2+2x=0,解得x1=0,x2=-2,
∴k的值为1或2.
点评 本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
16. 如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
 如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | (a+b)(a-b)=a2-b2 | D. | a(a-b)=a2-ab |
13.计算3a•2b的结果是( )
| A. | 3ab | B. | 5ab | C. | 6a | D. | 6ab |
12. 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )| A. | 2cm2 | B. | 1cm2 | C. | 0.5cm2 | D. | 0.25cm2 |
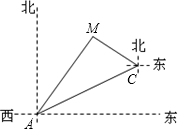 如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)
如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)