题目内容
13.在直角坐标系中有两条直线y=$\frac{3}{5}x+\frac{9}{5}$和y=-$\frac{3}{2}$x+6,它们的交点为P,第一条直线与x轴交于点A,第二条直线与x轴交于点B.求:(1)A,B两点的坐标;
(2)△PAB的面积.
分析 (1)利用图象与x轴相交,则y=0,分别求出A,B点坐标;
(2)将两函数联立求出交点坐标P点,进而利用三角形面积求法得出答案.
解答 解:(1)由y=$\frac{3}{5}x+\frac{9}{5}$,当y=0,解得:x=-3,
故A(-3,0),
由y=-$\frac{3}{2}$x+6,当y=0则,解得:x=4,
故B(4,0);
(2)如图所示:由题意可得:$\left\{\begin{array}{l}{y=\frac{3}{5}x+\frac{9}{5}}\\{y=-\frac{3}{2}x+6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
故P点坐标为:(2,3),
如图所示:S△PAB=$\frac{1}{2}$×7×3=$\frac{21}{2}$.
点评 此题主要考查了两直线相交问题以及三角形面积求法,正确得出两函数的交点坐标是解题关键.

练习册系列答案
相关题目
3.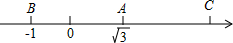 如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
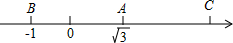 如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
 如图,AB⊥CD于点O,直线EF过点O,若∠AOE=55°,则∠DOF度数为35°.
如图,AB⊥CD于点O,直线EF过点O,若∠AOE=55°,则∠DOF度数为35°. 如图所示,BE平分∠ABC,DE∥BC,观察图中相等的角共有多少对?请你把它们都写出来.(用∠x=∠y的形式写具体)
如图所示,BE平分∠ABC,DE∥BC,观察图中相等的角共有多少对?请你把它们都写出来.(用∠x=∠y的形式写具体)