题目内容
在四边形ABCD中,如果∠A:∠B:∠C:∠D=1:2:3:4,则∠D=______
 144°
【解析】设∠A=x°,则∠B=2x°,∠C=3x°,∠D=4x°,
∵∠A+∠B+∠C+∠D=360°,
∴x+2x+3x+4x=360,
解得x=36°,
∴2x=72°,3x=108°,4x=144°,
所以∠A=36°,∠B=72°,∠C=108°,∠D=144°,
故答案为:144°.
144°
【解析】设∠A=x°,则∠B=2x°,∠C=3x°,∠D=4x°,
∵∠A+∠B+∠C+∠D=360°,
∴x+2x+3x+4x=360,
解得x=36°,
∴2x=72°,3x=108°,4x=144°,
所以∠A=36°,∠B=72°,∠C=108°,∠D=144°,
故答案为:144°.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若分式方程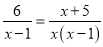 有增根,则增根是( )
有增根,则增根是( )
A. x=1 B. x=1或x=0 C. x=0 D. 不确定
 A
【解析】方程两边同乘x(x-1),得
6x=x+5,
解得:x=1,
检验:当x=1时,x(x-1)=0,所以x=1是原方程的增根,原方程无解,
故选A.
A
【解析】方程两边同乘x(x-1),得
6x=x+5,
解得:x=1,
检验:当x=1时,x(x-1)=0,所以x=1是原方程的增根,原方程无解,
故选A. 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
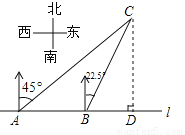
A. 4km B. (2+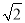 )km C. 2
)km C. 2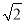 km D. (4-
km D. (4-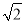 )km
)km
 B
【解析】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可得:BD=BE=km,因此CD=AD=AB+BD=(2+)km,故选B.
B
【解析】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可得:BD=BE=km,因此CD=AD=AB+BD=(2+)km,故选B. 如图,等腰梯形ABCD下底与上底的差恰好等于腰长,DE∥AB.则∠DEC等于( )
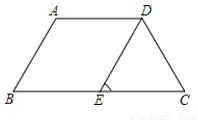
A. 75° B. 60° C. 45° D. 30°
 B
【解析】试题解析:∵DE∥AB,AD∥BC,
∴四边形ABED为平行四边形,
∴AD=BE,
∵BC-AD=AB=EC,
∵等腰梯形ABCD,
∴AB=DC=EC,
∴为等边三角形,
∴∠DEC=60°.
故选B.
B
【解析】试题解析:∵DE∥AB,AD∥BC,
∴四边形ABED为平行四边形,
∴AD=BE,
∵BC-AD=AB=EC,
∵等腰梯形ABCD,
∴AB=DC=EC,
∴为等边三角形,
∴∠DEC=60°.
故选B. 如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
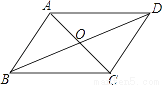
A. AO=OD B. AO⊥OD C. AO=OC D. AO⊥AB
 C
【解析】试题分析:对角线不一定相等,A错误;
对角线不一定互相垂直,B错误;
对角线互相平分,C正确;
对角线与边不一定垂直,D错误.
故选C.
C
【解析】试题分析:对角线不一定相等,A错误;
对角线不一定互相垂直,B错误;
对角线互相平分,C正确;
对角线与边不一定垂直,D错误.
故选C. 一个多边形的每个外角都是36°,这个多边形是______边形
 十
【解析】∵任何多边形的外角和等于360°,
∴多边形的边数为360°÷36°=10,
故答案为:十.
十
【解析】∵任何多边形的外角和等于360°,
∴多边形的边数为360°÷36°=10,
故答案为:十. 在多边形的内角中,锐角的个数不能多于( )
A. 2个 B. 3个 C. 4个 D. 5个
 B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B.
B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B. 若关于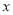 的方程
的方程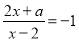 的解为正数,则
的解为正数,则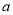 的取值范围是_____.
的取值范围是_____.
 且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且.
且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且. 化简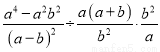 的结果是( )
的结果是( )
A. 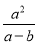 B.
B. 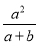 C.
C. 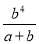 D.
D. 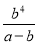
 D
【解析】试题解析:原式
故选D.
D
【解析】试题解析:原式
故选D. 
