题目内容
12．不等式组$\left\{\begin{array}{l}-x＜3\\ 2x-1≤3\end{array}\right.$的解集在数轴上表示正确的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 分别求出各不等式的解集，再在数轴上表示出来即可．
解答 解：$\left\{\begin{array}{l}-x＜3①\\ 2x-1≤3②\end{array}\right.$，
由①得，x＞-3，
由②得，x≤2，
故不等式组的解集为：-3＜x≤2，
在数轴上表示为：．
故选A．
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
3．定义：若点P（a，b）在函数y=$\frac{1}{x}$的图象上，将以a为二次项系数，b为一次项系数构造的二次函数y=ax2+bx称为函数y=$\frac{1}{x}$的一个“派生函数”．例如：点（2，$\frac{1}{2}$）在函数y=$\frac{1}{x}$的图象上，则函数y=2x2+$\frac{1}{2}x$称为函数y=$\frac{1}{x}$的一个“派生函数”．现给出以下两个命题：
（1）存在函数y=$\frac{1}{x}$的一个“派生函数”，其图象的对称轴在y轴的右侧
（2）函数y=$\frac{1}{x}$的所有“派生函数”，的图象都经过同一点，下列判断正确的是（ ）
（1）存在函数y=$\frac{1}{x}$的一个“派生函数”，其图象的对称轴在y轴的右侧
（2）函数y=$\frac{1}{x}$的所有“派生函数”，的图象都经过同一点，下列判断正确的是（ ）
| A． | 命题（1）与命题（2）都是真命题 | B． | 命题（1）与命题（2）都是假命题 | ||
| C． | 命题（1）是假命题，命题（2）是真命题 | D． | 命题（1）是真命题，命题（2）是假命题 |
20．六边形的内角和是（ ）
| A． | 540° | B． | 720° | C． | 900° | D． | 1080° |
7．若一组数据2，3，4，5，x的方差与另一组数据5，6，7，8，9的方差相等，则x的值为（ ）
| A． | 1 | B． | 6 | C． | 1或6 | D． | 5或6 |
如图，四边形ABCD内接于⊙O，AB是直径，过C点的切线与AB的延长线交于P点，若∠P=40°，则∠D的度数为115°．
4．
如图所示，AB是⊙O的直径，点C为⊙O外一点，CA，CD是⊙O的切线，A，D为切点，连接BD，AD．若∠ACD=30°，则∠DBA的大小是（ ）
如图所示，AB是⊙O的直径，点C为⊙O外一点，CA，CD是⊙O的切线，A，D为切点，连接BD，AD．若∠ACD=30°，则∠DBA的大小是（ ）| A． | 15° | B． | 30° | C． | 60° | D． | 75° |
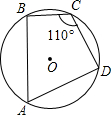如图，四边形ABCD为⊙O的内接四边形，已知∠BCD=110°，则∠BAD=70度．