题目内容
3.定义:若点P(a,b)在函数y=$\frac{1}{x}$的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=$\frac{1}{x}$的一个“派生函数”.例如:点(2,$\frac{1}{2}$)在函数y=$\frac{1}{x}$的图象上,则函数y=2x2+$\frac{1}{2}x$称为函数y=$\frac{1}{x}$的一个“派生函数”.现给出以下两个命题:(1)存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
| A. | 命题(1)与命题(2)都是真命题 | B. | 命题(1)与命题(2)都是假命题 | ||
| C. | 命题(1)是假命题,命题(2)是真命题 | D. | 命题(1)是真命题,命题(2)是假命题 |
分析 (1)根据二次函数y=ax2+bx的性质a、b同号对称轴在y轴左侧,a、b异号对称轴在y轴右侧即可判断.
(2)根据“派生函数”y=ax2+bx,x=0时,y=0,经过原点,即可得出结论.
解答 解:(1)∵P(a,b)在y=$\frac{1}{x}$上,
∴a和b同号,所以对称轴在y轴左侧,
∴存在函数y=$\frac{1}{x}$的一个“派生函数”,其图象的对称轴在y轴的右侧是假命题.
(2)∵函数y=$\frac{1}{x}$的所有“派生函数”为y=ax2+bx,
∴x=0时,y=0,
∴所有“派生函数”为y=ax2+bx经过原点,
∴函数y=$\frac{1}{x}$的所有“派生函数”,的图象都经过同一点,是真命题.
故选C.
点评 本题考查命题与定理、二次函数的性质,理解题意是解题的关键,记住二次函数y=ax2+bx的性质a、b同号对称轴在y轴左侧,a、b异号对称轴在y轴右侧,属于基础题.

练习册系列答案
相关题目
14.根据国家发改委实施“阶梯水价”的有关文件要求,某市结合地方实际,决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费,某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量,如表所示:
则这30户家庭该用用水量的众数和中位数分别是( )
| 用水量(吨) | 15 | 20 | 25 | 30 | 35 |
| 户数 | 3 | 6 | 7 | 9 | 5 |
| A. | 25,27 | B. | 25,25 | C. | 30,27 | D. | 30,25 |
15.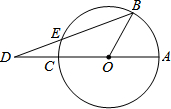 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )| A. | DE=EB | B. | $\sqrt{2}$DE=EB | C. | $\sqrt{3}$DE=DO | D. | DE=OB |
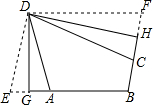 定义:有三个内角相等的四边形叫三等角四边形.
定义:有三个内角相等的四边形叫三等角四边形.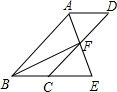 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E. 如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.