题目内容
20.六边形的内角和是( )| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
分析 多边形内角和定理:n变形的内角和等于(n-2)×180°(n≥3,且n为整数),据此计算可得.
解答 解:由内角和公式可得:(6-2)×180°=720°,
故选:B.
点评 此题主要考查了多边形内角和公式,关键是熟练掌握计算公式:(n-2)•180°(n≥3,且n为整数)..

练习册系列答案
相关题目
10.下列说法:
①三角形的三条高一定都在三角形内
②有一个角是直角的四边形是矩形
③有一组邻边相等的平行四边形是菱形
④两边及一角对应相等的两个三角形全等
⑤一组对边平行,另一组对边相等的四边形是平行四边形
其中正确的个数有( )
①三角形的三条高一定都在三角形内
②有一个角是直角的四边形是矩形
③有一组邻边相等的平行四边形是菱形
④两边及一角对应相等的两个三角形全等
⑤一组对边平行,另一组对边相等的四边形是平行四边形
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.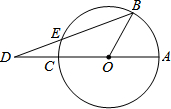 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )| A. | DE=EB | B. | $\sqrt{2}$DE=EB | C. | $\sqrt{3}$DE=DO | D. | DE=OB |
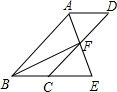 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
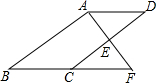 如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.


