题目内容
4. 如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )| A. | 15° | B. | 30° | C. | 60° | D. | 75° |
分析 首先连接OD,由CA,CD是⊙O的切线,∠ACD=30°,即可求得∠AOD的度数,又由OB=OD,即可求得答案.
解答  解:连接OD,
解:连接OD,
∵CA,CD是⊙O的切线,
∴OA⊥AC,OD⊥CD,
∴∠OAC=∠ODC=90°,
∵∠ACD=30°,
∴∠AOD=360°-∠C-∠OAC-∠ODC=150°,
∵OB=OD,
∴∠DBA=∠ODB=$\frac{1}{2}$∠AOD=75°.
故选D.
点评 此题考查了切线的性质以及等腰三角形的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
14.根据国家发改委实施“阶梯水价”的有关文件要求,某市结合地方实际,决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费,某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量,如表所示:
则这30户家庭该用用水量的众数和中位数分别是( )
| 用水量(吨) | 15 | 20 | 25 | 30 | 35 |
| 户数 | 3 | 6 | 7 | 9 | 5 |
| A. | 25,27 | B. | 25,25 | C. | 30,27 | D. | 30,25 |
15.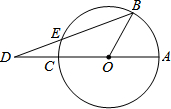 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )| A. | DE=EB | B. | $\sqrt{2}$DE=EB | C. | $\sqrt{3}$DE=DO | D. | DE=OB |
19.-$\sqrt{2}$的相反数是( )
| A. | $\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | -2 |
9.已知等腰三角形的一边长为8,另一边长为5,则它的周长为( )
| A. | 18 | B. | 21 | C. | 13或21 | D. | 18或21 |



