题目内容
17. 如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为115°.
如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为115°.
分析 根据过C点的切线与AB的延长线交于P点,∠P=40°,可以求得∠OCP和∠OBC的度数,又根据圆内接四边形对角互补,可以求得∠D的度数,本题得以解决.
解答  解:连接OC,如右图所示,
解:连接OC,如右图所示,
由题意可得,∠OCP=90°,∠P=40°,
∴∠COB=50°,
∵OC=OB,
∴∠OCB=∠OBC=65°,
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=115°,
故答案为:115°.
点评 本题考查切线的性质、圆内接四边形,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.分式方程$\frac{3}{x}$=$\frac{4}{x+1}$的解是( )
| A. | x=-1 | B. | x=1 | C. | x=2 | D. | x=3 |
2.若2x2my3与-5xy2n是同类项,则|m-n|的值是( )
| A. | 0 | B. | 1 | C. | 7 | D. | -1 |
 如图,在⊙O中,弦AC=2$\sqrt{3}$,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=$\sqrt{6}$.
如图,在⊙O中,弦AC=2$\sqrt{3}$,点B是圆上一点,且∠ABC=45°,则⊙O的半径R=$\sqrt{6}$.
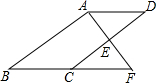 如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.