题目内容
12.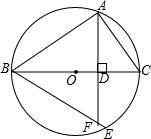 如图,BC是⊙O的直径,点A、E均在⊙0上,且位于直径BC的两侧,$\widehat{AE}$=$\widehat{AB}$,AD⊥BC于点D,BE交AD的延长线于点F.
如图,BC是⊙O的直径,点A、E均在⊙0上,且位于直径BC的两侧,$\widehat{AE}$=$\widehat{AB}$,AD⊥BC于点D,BE交AD的延长线于点F.(1)∠ACB与∠BAD相等吗?为什么?
(2)小明发现:点O是△ABF的垂心,你认为小明的发现正确吗?请说明理由.
分析 (1)根据圆周角定理和等角的余角相等即可证得;
(2)连接AO,并延长交BE于G,根据等腰三角形的性质和圆周角定理得出∠ACB=∠OAC,∠ABE=∠ACB,进而即可证得∠ABE+∠BAG=90°,证得∠AGB=90°,即可证得点O是△ABF的垂心.
解答  解:(1)相等,
解:(1)相等,
理由;∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠BAD+∠DAC=90°,
∵AD⊥BC,
∴∠ACB+∠DAC=90°,
∴∠ACB=∠BAD;
(2)连接AO,并延长交BE于G,如图,
∵OA=OC,
∴∠ACB=∠OAC,
∵∠OAC+∠BAG=90°,
∴ACB+∠BAG=90°,
∵$\widehat{AE}$=$\widehat{AB}$,
∴∠ABE=∠ACB,
∴∠ABE+∠BAG=90°,
∴∠AGB=90°,
即AG⊥BF,
∵BD⊥AF,且BD经过O点,AG经过O点,
∴点O是△ABF的垂心.
点评 本题考查了圆周角定理,等腰三角形的性质,等角的余角相等等,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
17.x>-y,则下列不等式中成立的有( )
| A. | x+y<0 | B. | x-y>0 | C. | a2x>-a2y | D. | 3x+3y>0 |
 已知AD,BC相交于点O,AB=CD,∠ABC=∠CDA,求证:∠A=∠C.
已知AD,BC相交于点O,AB=CD,∠ABC=∠CDA,求证:∠A=∠C.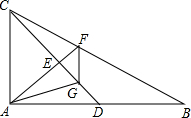 如图,在Rt△ABC中,E为CD的中点,FG∥AC.
如图,在Rt△ABC中,E为CD的中点,FG∥AC.