题目内容
20.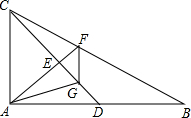 如图,在Rt△ABC中,E为CD的中点,FG∥AC.
如图,在Rt△ABC中,E为CD的中点,FG∥AC.(1)若BD=DA,试探究AG与BF数量关系;
(2)若BD=kDA,AG与BF数量关系如何,加以证明.
分析 (1)过点B作BN∥AC,与AF延长线交于N,过D作DM∥AC,由AE是Rt△ACD斜边的中线,得到AE=CE=DE,推出△ACE∽△FGE,得到△EFG是等腰三角形,证得AF=CG,推出△AGC≌△CFA,根据全等三角形的性质得到AG=CF,根据平行线的性质得到∠EAC=∠EMD,推出△AEC≌△MED,证得AC=MD,根据相似三角形的性质得到$\frac{AD}{AB}=\frac{MD}{BN}=\frac{1}{2}$,求得$\frac{AC}{BN}=\frac{1}{2}$,根据相似三角形的性质即可得到结论;
(2)设DA=a,则BD=ka,则AB=(1+k)a,推出$\frac{DM}{BN}=\frac{AD}{AB}$,于是得到$\frac{AC}{BN}=\frac{a}{(1+k)a}=\frac{1}{1+k}$,证得$\frac{CF}{BF}=\frac{AC}{BN}=\frac{1}{1+k}$,即BF=(1+k)CF,于是得到结论.
解答 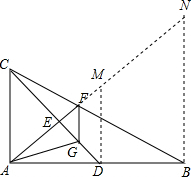 解:(1)BF=2AG,
解:(1)BF=2AG,
证明:过点B作BN∥AC,与AF延长线交于N,过D作DM∥AC,
∵AE是Rt△ACD斜边的中线,
∴AE=CE=DE,
∵FG∥AC,
∴△ACE∽△FGE,
∴△EFG是等腰三角形,
∴EF=EG,
∴AE+EF=CE+EG,
∴AF=CG,
在△AGC和△CFA中,$\left\{\begin{array}{l}{AC=AC}\\{∠ECA=∠EAC}\\{CG=AF}\end{array}\right.$,
∴△AGC≌△CFA,
∴AG=CF,DM∥BN∥AC,
∴∠EAC=∠EMD,
在△AEC与△MED中,$\left\{\begin{array}{l}{∠EAC=∠EMD}\\{∠AEC=∠DEM}\\{CE=DE}\end{array}\right.$,
∴△AEC≌△MED,
∴AC=MD,
∴△AMD∽△ANB,
∴$\frac{AD}{AB}=\frac{MD}{BN}=\frac{1}{2}$,
∴$\frac{AC}{BN}=\frac{1}{2}$,
∴△ACF∽△NBF,
∴$\frac{CF}{BF}=\frac{AC}{BN}=\frac{1}{2}$,
∴BF=2CF=2AG;
(2)BD=kDA,设DA=a,
则BD=ka,则AB=(1+k)a,
∴$\frac{DM}{BN}=\frac{AD}{AB}$,
即$\frac{AC}{BN}=\frac{a}{(1+k)a}=\frac{1}{1+k}$,
∴$\frac{CF}{BF}=\frac{AC}{BN}=\frac{1}{1+k}$,
即BF=(1+k)CF,
∴BF=(k+1)AG.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,平行线的性质,正确的作出辅助线是解题的关键.

| A. | 1 | B. | 0 | C. | -1 | D. | -$\frac{1}{2}$ |
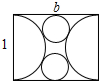 如图,用邻边分别为1,b(b>1)的矩形硬纸板裁出以1为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥的侧面,小圆恰好作为底面,从而做成两个圆锥(拼接处材料忽略不计),则b的值为( )
如图,用邻边分别为1,b(b>1)的矩形硬纸板裁出以1为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥的侧面,小圆恰好作为底面,从而做成两个圆锥(拼接处材料忽略不计),则b的值为( )| A. | b=$\sqrt{3}$ | B. | b=$\frac{\sqrt{5}+1}{2}$ | C. | b=$\frac{\sqrt{5}}{2}$ | D. | b=$\sqrt{2}$ |
| A. | 1,1,$\sqrt{2}$ | B. | 2,5,6 | C. | 3,4,5 | D. | 5,12,13 |
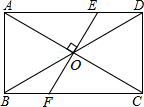 如图,矩形ABCD中,AB=3,BC=5,AC、BD交于点O.过O作EF⊥AC交AD于E,交BC于F.
如图,矩形ABCD中,AB=3,BC=5,AC、BD交于点O.过O作EF⊥AC交AD于E,交BC于F.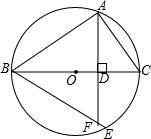 如图,BC是⊙O的直径,点A、E均在⊙0上,且位于直径BC的两侧,$\widehat{AE}$=$\widehat{AB}$,AD⊥BC于点D,BE交AD的延长线于点F.
如图,BC是⊙O的直径,点A、E均在⊙0上,且位于直径BC的两侧,$\widehat{AE}$=$\widehat{AB}$,AD⊥BC于点D,BE交AD的延长线于点F.