题目内容
15.我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg-5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)当x=2200时,方案A和方案B哪种方案付款少?
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,他应选择哪种方案?
分析 (1)根据题意,可以分别表示出方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)根据(1)中的函数解析式,将x=2200代入,求出相应的函数值,然后再比较大小,即可解答本题;
(3)根据(1)中的函数解析式可以分别求得用20000元,两种方案各购买多少苹果,然后比较大小,即可解答本题.
解答 解:(1)由题意可得,
方案A购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式:y=5.8x,
方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式:y=5x+2000;
(2)当x=2200时,
方案A:y=5.8×2200=12760(元),
方案B:y=5×2200+2000=13000(元),
∵12760<13000,
∴方案A付款少;
(3)由题意可得,
方案A可以购买的苹果数量为:20000÷5.8≈3448(kg),
方案B可以购买的苹果数量为:(20000-2000)÷5=3600(kg),
∵3600>3448,
∴他应选择方案B购买.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用函数的性质解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
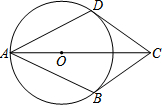 如图,已知在四边形ABCD中,AB=AD,BC=CD,点O在对角线AC上,以O为圆心OA为半径的⊙O与CD相切于点D.
如图,已知在四边形ABCD中,AB=AD,BC=CD,点O在对角线AC上,以O为圆心OA为半径的⊙O与CD相切于点D.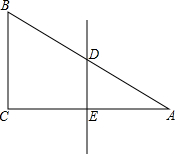 如图,△ABC中,AC的中垂线交AB,AC于点D,E,点D是AB的中点,判断△ABC的形状,并写出理由.
如图,△ABC中,AC的中垂线交AB,AC于点D,E,点D是AB的中点,判断△ABC的形状,并写出理由.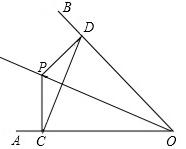 如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D. 如图,△ABC中,已知MN∥BC分别交AB、AC于点M、N,DN∥MC交AB于点D.
如图,△ABC中,已知MN∥BC分别交AB、AC于点M、N,DN∥MC交AB于点D.