Question

5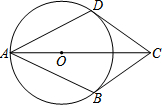．如图，已知在四边形ABCD中，AB=AD，BC=CD，点O在对角线AC上，以O为圆心OA为半径的⊙O与CD相切于点D．
（1）求证：直线BC是⊙O的切线；
（2）若⊙O的半径为6，CD=8，求弦AD的长．

Answer 1

分析 （1）连接OD，OB，根据全等三角形的性质得到∠1=∠2，根据切线的性质得到∠ODC=90°，根据全等三角形的性质得到∠OBC=∠ODC=90°，于是得到结论；
（2）过D作DE⊥AC于E，根据勾股定理得到OC=10，根据三角形的面积公式得到DE=$\frac{OD•CD}{OC}$=$\frac{24}{5}$，根据射影定理得到OD²=OE•OC，求得OE=$\frac{36}{10}$=$\frac{18}{5}$，根据勾股定理即可得到结论．

解答 解：（1）连接OD，OB，
在△ADC与△ABC中，$\left\{\begin{array}{l}{AD=AB}\\{CD=CB}\\{AC=AC}\end{array}\right.$，
∴△ADC≌△ABC，
∴∠1=∠2，
∵CD是⊙O的切线，
∴∠ODC=90°，
在△CDO与△CBO中，$\left\{\begin{array}{l}{CD=CB}\\{∠1=∠2}\\{OC=OC}\end{array}\right.$，
∴△CDO≌△CBO，
∴∠OBC=∠ODC=90°，
∴OB⊥CB，
∴直线BC是⊙O的切线；

（2）过D作DE⊥AC于E，
∵∠ODC=90°，OD=6，CD=8，
∴OC=10，
∴DE=$\frac{OD•CD}{OC}$=$\frac{24}{5}$，
∵∠ODC=90°，DE⊥OC，
∴OD²=OE•OC，
∴OE=$\frac{36}{10}$=$\frac{18}{5}$，
∴AE=$\frac{48}{5}$，
∴AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=$\sqrt{（\frac{24}{5}）^{2}+（\frac{48}{5}）^{2}}$=$\frac{24\sqrt{5}}{5}$．

点评 本题考查了切线的判定和性质，全等三角形的判断和性质，射影定理，勾股定理，正确的作出辅助线是解题的关键．