题目内容
7.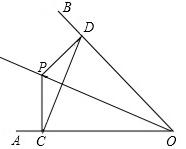 如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.(1)∠PCD=∠PDC吗?为什么?
(2)试说明OD=OC.
分析 (1)∠PCD=∠PDC.由于P点是∠AOB平分线上一点,根据角平分线的性质可以推出PC=PD,然后利用等腰三角形的性质即可得到结论;
(2)根据已知条件首先容易证明Rt△POC≌Rt△POD,从而得到OC=OD.
解答 解:(1)∠PCD=∠PDC.
理由:∵OP是∠AOB的平分线,
且PC⊥OA,PD⊥OB,
∴PC=PD,
∴∠PCD=∠PDC;
(2)∵∠OCP=∠ODP=90°,
在Rt△POC和Rt△POD中,
$\left\{\begin{array}{l}{PC=PD}\\{OP=OP}\end{array}\right.$,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD.
点评 此题主要考查了角平分线的性质,利用它构造全等三角形来解决问题.

练习册系列答案
相关题目
17.下列各式中,没有意义的是( )
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{(-2)^{2}}$ | C. | $\sqrt{-\frac{1}{3}}$ | D. | $-\sqrt{2}$ |
 将连接的偶数2,4,6,8,…排成如下的数表,用一个十字形框中五个数.
将连接的偶数2,4,6,8,…排成如下的数表,用一个十字形框中五个数.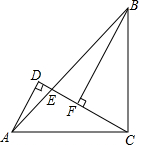 如图所示,△ADC是直角三角形,∠ADC=90°,AC=BC,且AC⊥BC于点C,BF⊥CD于F,连接AB交CD于E,试说明:AD+DF=BF.
如图所示,△ADC是直角三角形,∠ADC=90°,AC=BC,且AC⊥BC于点C,BF⊥CD于F,连接AB交CD于E,试说明:AD+DF=BF. 应用一元二次方程解答下列问题:
应用一元二次方程解答下列问题: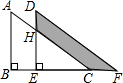 如图,将直角三角形ABC沿直线BC向右平移后,到达三角形DEF位置,如果AB=8cm,BE=4cm,DH=3cm,求图中阴影部分面积.
如图,将直角三角形ABC沿直线BC向右平移后,到达三角形DEF位置,如果AB=8cm,BE=4cm,DH=3cm,求图中阴影部分面积.