题目内容
6.若一次函数y=3x+6与一次函数y=2x-4的图象的交点为(a,b),则$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是下列哪个方程组的解( )| A. | $\left\{\begin{array}{l}{3x-y=-6}\\{2x-y-4=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+6+y=0}\\{2x-y-y=0}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y-3x=6}\\{2x+y=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x-y=6}\\{2x-y=4}\end{array}\right.$ |
分析 由于函数图象交点坐标为两函数解析式组成的方程组的解,因此联立两函数解析式所得方程组的解,就是两个函数图象的交点坐标.
解答 解:因为一次函数y=3x+6与一次函数y=2x-4的图象的交点为(a,b),
所以$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{3x-y=-6}\\{2x-y=4}\end{array}\right.$的解,
故选A
点评 此题考查一次函数与二元一次方程组关系,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | $\frac{1}{81}$的立方根是$\frac{1}{9}$ | B. | -$\frac{1}{81}$的平方根是$\frac{1}{9}$ | ||
| C. | $\frac{1}{27}$的算术平方根是$\frac{1}{3}$ | D. | -$\frac{1}{27}$的立方根是-$\frac{1}{3}$ |

 如图,已知a、b、c在数轴上的位置,化简:|a-b|-|b-c|+|c-a|=2b-2a.
如图,已知a、b、c在数轴上的位置,化简:|a-b|-|b-c|+|c-a|=2b-2a.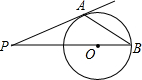 如图,PA切⊙O于A,PO交⊙O于B,若∠P=35°,则∠PBA=27.5°.
如图,PA切⊙O于A,PO交⊙O于B,若∠P=35°,则∠PBA=27.5°.