题目内容
18.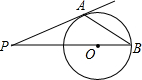 如图,PA切⊙O于A,PO交⊙O于B,若∠P=35°,则∠PBA=27.5°.
如图,PA切⊙O于A,PO交⊙O于B,若∠P=35°,则∠PBA=27.5°.
分析 连结OA,如图,先根据切线性质得∠OAP=90°,则利用互余可计算出∠POA=55°,加上∠B=∠OAB,然后利用三角形外角性质可计算出∠B的度数.
解答 解:连结OA,如图,
∵PA切⊙O于A,
∴OA⊥PA,
∴∠OAP=90°,
∴∠POA=90°-∠P=90°-35°=55°,
∵OA=OB,
∴∠B=∠OAB,
而∠POA=∠B+∠OAB,
∴∠B=$\frac{1}{2}$∠POA=27.5°.
故答案为27.5°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若一次函数y=3x+6与一次函数y=2x-4的图象的交点为(a,b),则$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是下列哪个方程组的解( )
| A. | $\left\{\begin{array}{l}{3x-y=-6}\\{2x-y-4=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+6+y=0}\\{2x-y-y=0}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y-3x=6}\\{2x+y=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x-y=6}\\{2x-y=4}\end{array}\right.$ |
3.要使四边形ABCD的中点四边形为菱形,则四边形ABCD( )
| A. | 一定为菱形 | B. | 一定为矩形 | C. | 只需对角线相等 | D. | 只需对角线垂直 |
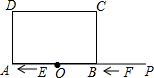 如图,长方形ABCD中,AB=6,BC=2$\sqrt{3}$,∠DCA=30°.点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和长方形ABCD在射线PA的同侧,设运动的时间为t秒(t≥0).
如图,长方形ABCD中,AB=6,BC=2$\sqrt{3}$,∠DCA=30°.点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和长方形ABCD在射线PA的同侧,设运动的时间为t秒(t≥0). 如图,Rt△ACD中,∠C=90°,∠CAD=60°,∠CAD的平分线AB交CD于B点,且AB=4cm,那么点B到AD的距离是2cm.
如图,Rt△ACD中,∠C=90°,∠CAD=60°,∠CAD的平分线AB交CD于B点,且AB=4cm,那么点B到AD的距离是2cm. 观察函数y=x2-3x+2的图象,回答下列问题:
观察函数y=x2-3x+2的图象,回答下列问题: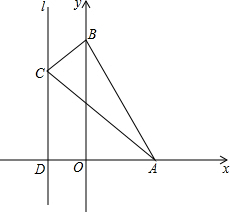 在平面直角坐标系xOy中,点A的坐标为(2,0),点B的坐标为(0,4),直线l经过(-1,0)并且与x轴垂直于点D,请你在直线l上找一点C,使△ABC为直角三角形,并求出点C的坐标.
在平面直角坐标系xOy中,点A的坐标为(2,0),点B的坐标为(0,4),直线l经过(-1,0)并且与x轴垂直于点D,请你在直线l上找一点C,使△ABC为直角三角形,并求出点C的坐标.