题目内容
16．如图，正方形内数字分别为所在正方形的面积，则图中字母A，B，C所代表的正方形面积是81，64，100．
分析 根据勾股定理，即可求出A，B，C所代表的正方形的面积．
解答 解：如图1所示：
∵∠DEF=90°，
∴DE2=DF2-EF2=162-81=81，
∴字母A所代表的正方形面积是81；
同理：字母B所代表的正方形面积=172-152=64；
字母C所代表的正方形面积=64+36=100；
故答案为：81，64，100．
点评 本题考查了勾股定理；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
4．（1）计算：2sin30°+$\sqrt{2}$•$\sqrt{8}$-（2-π）0-（$\frac{1}{2}$）-1．
（2）解方程：$\frac{1}{x-2}$=$\frac{3}{x}$．
（2）解方程：$\frac{1}{x-2}$=$\frac{3}{x}$．
11．全年生产总值达480.14亿元，其中480.14亿元用科学记数法保留三个有效数字可表示为（ ）
| A． | 480×108元 | B． | 4.8×1010元 | C． | 4.80×1010元 | D． | 4.80××108元 |
如图，DE是△ABC的中位线，且DE=7cm，GH是梯形DECB的中位线，则GH=10.5cm．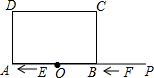
如图，长方形ABCD中，AB=6，BC=2$\sqrt{3}$，∠DCA=30°．点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动．在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和长方形ABCD在射线PA的同侧，设运动的时间为t秒（t≥0）．
6．若一次函数y=3x+6与一次函数y=2x-4的图象的交点为（a，b），则$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是下列哪个方程组的解（ ）
| A． | $\left\{\begin{array}{l}{3x-y=-6}\\{2x-y-4=0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{3x+6+y=0}\\{2x-y-y=0}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{y-3x=6}\\{2x+y=-4}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{3x-y=6}\\{2x-y=4}\end{array}\right.$ |