题目内容
9. 如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)
如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)(1)请你帮小明计算一下学校教学楼的高度;
(2)为了迎接上级领导检查,学校准备在AE之间挂一些彩旗,请计算AE之间的长.(结果精确到1m,参考数据:sin22°≈0.375,cos22°≈0.9375,tan22°≈0.4)
分析 (1)首先构造直角三角形△AEM,利用tan22°=$\frac{AM}{ME}$,即可求出教学楼AB的高度;
(2)利用Rt△AME中,cos22°=$\frac{ME}{AE}$,求出AE即可.
解答 解:(1)过点E作EM⊥AB,垂足为M.设AB为xm,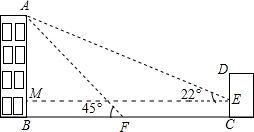
在Rt△ABF中,∠AFB=45°,
∴BF=AB=xm,
∴BC=BF+FC=(x+13)m,
在Rt△AEM中,AM=AB-BM=AB-CE=(x-2)m,
又tan∠AEM=$\frac{AM}{ME}$,∠AEM=22°,
∴$\frac{x-2}{x+13}$=0.4,解得x≈12,
故学校教学楼的高度约为12m;
(2)由(1),得ME=BC=BF+13≈12+13=25(m).…(6分)
在Rt△AEM中,cos∠AEM=$\frac{ME}{AE}$,
∴AE=$\frac{ME}{cos22°}$≈$\frac{25}{0.9375}$≈27(m),
故AE的长约为27m.
点评 此题主要考查了解直角三角形的应用,根据已知得出tan22°=$\frac{AM}{ME}$是解题关键.

练习册系列答案
相关题目
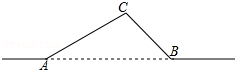 如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米,
如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米, 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在点C的深度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1)
由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在点C的深度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1)