��Ŀ����
14������$\frac{1}{x}$+$\frac{x}{1}$=2�Ľ���x=1��$\frac{2}{x}$+$\frac{x}{2}$=2�Ľ���x=2��$\frac{3}{x}$+$\frac{x}{3}$=2�Ľ���x=3��-$\frac{2}{x}$-$\frac{x}{2}$=2����$\frac{-2}{x}$+$\frac{x}{-2}$=2���Ľ���x=-2���۲��������������������������x�ķ���$\frac{m}{x}$+$\frac{x}{m}$=2��m��0���Ľ⣬�����á����̵Ľ⡱�ĸ��������֤��
���� ����֪���Ķ����ϣ�����$\frac{1}{x}$+$\frac{x}{1}$=2�Ľ���x=1��$\frac{2}{x}$+$\frac{x}{2}$=2�Ľ���x=2��$\frac{3}{x}$+$\frac{x}{3}$=2�Ľ���x=3��-$\frac{2}{x}$-$\frac{x}{2}$=2����$\frac{-2}{x}$+$\frac{x}{-2}$=2���Ľ���x=-2�����ɿɵ÷���$\frac{m}{x}$+$\frac{x}{m}$=2��m��0���Ľ���x=m�����÷��̽�ĸ�������֤�����ۣ�
��� �⣺����֪�У�����$\frac{1}{x}$+$\frac{x}{1}$=2�Ľ���x=1��
$\frac{2}{x}$+$\frac{x}{2}$=2�Ľ���x=2��
$\frac{3}{x}$+$\frac{x}{3}$=2�Ľ���x=3��
-$\frac{2}{x}$-$\frac{x}{2}$=2����$\frac{-2}{x}$+$\frac{x}{-2}$=2���Ľ���x=-2��
��
���ɿɵ÷���$\frac{m}{x}$+$\frac{x}{m}$=2��m��0���Ľ���x=m��
��֤��
��x=m����ã����=$\frac{m}{m}$+$\frac{m}{m}$=1+1=2=�ұߣ�
��m�Ƿ���$\frac{m}{x}$+$\frac{x}{m}$=2�Ľ⣮
���� ������Ҫ�����ʽ���̵Ľ⣬���̵Ľ⼴Ϊ��ʹ����������ȵ�δ֪����ֵ��

��ϰ��ϵ�д�
 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
�����Ŀ
6�� ��ͼ����һ�ž���ֽƬABCD�У�AB=4��BC=8����E��F�ֱ���AD��BC�ϣ���ֽƬ
��ͼ����һ�ž���ֽƬABCD�У�AB=4��BC=8����E��F�ֱ���AD��BC�ϣ���ֽƬ
ABCD��ֱ��EF�۵�����C����AD�ϵ�һ��H������D���ڵ�G�����������ĸ����ۣ�
���ı���CFHE�����Σ���ECƽ�֡�DCH�����߶�BF��ȡֵ��ΧΪ3��BF��4��
�ܵ���H���A�غ�ʱ��EF=2$\sqrt{5}$�����Ͻ����У�����Ϊ��ȷ���ǣ�������
 ��ͼ����һ�ž���ֽƬABCD�У�AB=4��BC=8����E��F�ֱ���AD��BC�ϣ���ֽƬ
��ͼ����һ�ž���ֽƬABCD�У�AB=4��BC=8����E��F�ֱ���AD��BC�ϣ���ֽƬABCD��ֱ��EF�۵�����C����AD�ϵ�һ��H������D���ڵ�G�����������ĸ����ۣ�
���ı���CFHE�����Σ���ECƽ�֡�DCH�����߶�BF��ȡֵ��ΧΪ3��BF��4��
�ܵ���H���A�غ�ʱ��EF=2$\sqrt{5}$�����Ͻ����У�����Ϊ��ȷ���ǣ�������
| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �٢ۢ� | D�� | �ڢۢ� |
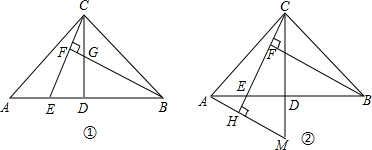
 ��ͼ��С�������ѧУ��ѧ¥�ĸ߶ȣ���ѧ¥AB�ĺ�����һ������CD������õ�����������22��ļн�ʱ����ѧ¥�ڽ������ǽ�����¸�2m�ߵ�Ӱ��CE����������������45��ļн�ʱ����ѧ¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��13m�ľ��루��B��F��C��ͬһ��ֱ���ϣ�
��ͼ��С�������ѧУ��ѧ¥�ĸ߶ȣ���ѧ¥AB�ĺ�����һ������CD������õ�����������22��ļн�ʱ����ѧ¥�ڽ������ǽ�����¸�2m�ߵ�Ӱ��CE����������������45��ļн�ʱ����ѧ¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��13m�ľ��루��B��F��C��ͬһ��ֱ���ϣ�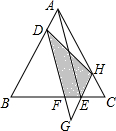 ��ͼ����ABC���������Σ�D��E�ֱ���AB��BC�ϵĵ㣬����CE=$\frac{1}{4}$CB����AD��AEΪ�ڱ�������һ��ƽ���ı���ADGE��DG��BC�ڵ�F���ӳ�GE��AC�ڵ�H������DH����S��BDF=9��S��GEF=1��ô�ı���DFEH�����Ϊ��������
��ͼ����ABC���������Σ�D��E�ֱ���AB��BC�ϵĵ㣬����CE=$\frac{1}{4}$CB����AD��AEΪ�ڱ�������һ��ƽ���ı���ADGE��DG��BC�ڵ�F���ӳ�GE��AC�ڵ�H������DH����S��BDF=9��S��GEF=1��ô�ı���DFEH�����Ϊ��������