题目内容
19.化简:(1)(x-y)(3x-y)-(x-2y)2+5y2
(2)$\frac{1}{y}-\frac{y-3}{y-2}÷(y+2-\frac{5}{y-2})$.
分析 (1)先算乘法,再合并同类项即可;
(2)先算括号内的减法,再把除法变成乘法,算乘法,最后算减法即可.
解答 解:(1)原式=3x2-xy-3xy+y2-x2+4xy-4y2+5y2
=2x2-2y2;
(2)原式=$\frac{1}{y}$-$\frac{y-3}{y-2}$÷[$\frac{(y+2)(y-2)}{y-2}$-$\frac{5}{y-2}$]
=$\frac{1}{y}$-$\frac{y-3}{y-2}$÷$\frac{{y}^{2}-9}{y-2}$
=$\frac{1}{y}$-$\frac{y-3}{y-2}$•$\frac{y-2}{(y+3)(y-3)}$
=$\frac{1}{y}$-$\frac{1}{y+3}$
=$\frac{y+3-y}{y(y+3)}$
=$\frac{3}{y(y+3)}$.
点评 本题考查了整式的混合运算和分式的混合运算的应用,能熟记运算法则是解此题的关键,注意运算顺序.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
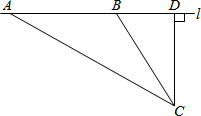 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. 如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)
如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)