题目内容
17.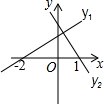 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )| A. | x<-2 | B. | -2<x<1 | C. | x>0 | D. | x>1 |
分析 观察函数图象得到当x>1时,不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$符合.
解答 解:当x>1时,符合不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$.
故选D
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
8.用换元法解方程:$\frac{{x}^{2}-2}{x}$+$\frac{2x}{{x}^{2}-2}$=3时,若设$\frac{{x}^{2}-2}{x}=y$,并将原方程化为关于y的整式方程,那么这个整式方程是( )
| A. | y2-3y+2=0 | B. | y2-3y-2=0 | C. | y2+3y+2=0 | D. | y2+3y-2=0 |
7. 如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )
如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )
 如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )
如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
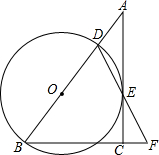 在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O.与AC相切于点E,连结DE并延长与BC的延长线交于点F.
在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O.与AC相切于点E,连结DE并延长与BC的延长线交于点F.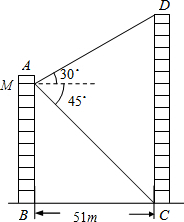 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)
如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)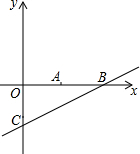 在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).
在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5). 如图,AB=6,将以AB为直径的半圆再绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为$\frac{9}{2}$π.
如图,AB=6,将以AB为直径的半圆再绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为$\frac{9}{2}$π.