题目内容
2.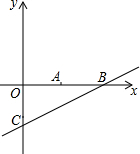 在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).
在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).(1)求过B、C两点的一次函数解析式;
(2)若直线BC上有一动点P(m,n),以点O、A、P为顶点的三角形面积和以点O、C、P为顶点的三角形面积相等,求P点坐标;
(3)若y轴上有一动点Q,使以点Q、A、C为顶点的三角形为等腰三角形,直接写出Q点坐标.
分析 (1)设直线BC解析式为y=kx+b,把B与C坐标代入求出k与b的值,即可确定出解析式;
(2)由P的坐标,根据三角形OAP与三角形OCP面积相等找出m与n的关系式,代入直线BC解析式求出m与n的值,即可确定出P的坐标;
(3)如图所示,分四种情况考虑:当CQ1=AQ1=5时,此时Q1与原点O重合;当AC=AQ2=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$时,求出此时OQ2的长,确定出Q2坐标;当AC=CQ3=5$\sqrt{2}$时,OQ3=OC+CQ3=5+5$\sqrt{2}$,求出此时Q3坐标;当AC=CQ4=5$\sqrt{2}$时,求出此时Q4坐标即可.
解答 解:(1)设一次函数解析式为y=kx+b,
把B(10,0)和C(0,-5)代入得:$\left\{\begin{array}{l}{10k+b=0}\\{b=-5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-5}\end{array}\right.$,
则一次函数解析式为y=$\frac{1}{2}$x-5;
(2)∵P坐标为(m,n),且S△OAP=S△OCP,OA=OC=5,
∴$\frac{1}{2}$OA•|n|=$\frac{1}{2}$OC•|m|,即|n|=|m|,
∴m=±n,
当m=n时,代入y=$\frac{1}{2}$x-5得:m=$\frac{1}{2}$m-5,即m=-10,此时P(-10,-10);
当m=-n时,代入y=$\frac{1}{2}$x-5得:-m=$\frac{1}{2}$m-5,即m=$\frac{10}{3}$,n=-$\frac{10}{3}$,此时P($\frac{10}{3}$,-$\frac{10}{3}$);
(3)如图所示,分四种情况考虑: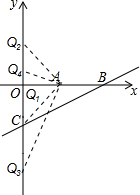
当CQ1=AQ1=5时,此时Q1与原点O重合,即Q1坐标为(0,0);
当AC=AQ2=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$时,此时OQ2=5,即Q2坐标为(0,5);
当AC=CQ3=5$\sqrt{2}$时,OQ3=OC+CQ3=5+5$\sqrt{2}$,此时Q3坐标为(0,-5-5$\sqrt{2}$);
当AC=CQ4=5$\sqrt{2}$时,OQ4=CQ4-OC=5$\sqrt{2}$-5,此时Q4坐标为(0,5$\sqrt{2}$-5),
综上,Q的坐标为(0,0)或(0,5)或(0,-5-5$\sqrt{2}$)或(0,5$\sqrt{2}$-5).
点评 此题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,等腰三角形的性质,坐标与图形性质,以及三角形的面积,熟练掌握待定系数法是解本题的关键.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案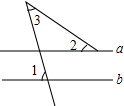 如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )
如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )| A. | 75° | B. | 50° | C. | 35° | D. | 30° |
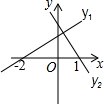 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )| A. | x<-2 | B. | -2<x<1 | C. | x>0 | D. | x>1 |

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
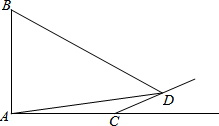 如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:$\sqrt{3}$,求旗杆AB的高度($\sqrt{3}≈1.7$,结果精确到个位).
如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:$\sqrt{3}$,求旗杆AB的高度($\sqrt{3}≈1.7$,结果精确到个位).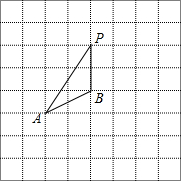 如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.
如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上. 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).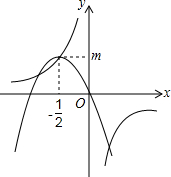 如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.
如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.