题目内容
6. 如图,AB=6,将以AB为直径的半圆再绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为$\frac{9}{2}$π.
如图,AB=6,将以AB为直径的半圆再绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为$\frac{9}{2}$π.
分析 先根据旋转的性质得S半圆AB=S半圆A′B,∠ABA′=45°,再利用面积的和差得到S阴影部分+S半圆AB=S半圆A′B+S扇形ABA′,即有S阴影部分=S扇形ABA′,然后根据扇形的面积公式计算即可.
解答 解:∵半圆AB绕点B顺时针旋转45°,点A旋转到A′的位置,
∴S半圆AB=S半圆A′B,∠ABA′=45°,
∵S阴影部分+S半圆AB=S半圆A′B+S扇形ABA′,
∴S阴影部分=S扇形ABA′=$\frac{45π•{6}^{2}}{360}$=$\frac{9π}{2}$.
故答案为:$\frac{9}{2}$π.
点评 本题考查了扇形面积的计算:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=$\frac{360}{n}$πR2或S扇形=$\frac{1}{2}$lR(其中l为扇形的弧长).

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
17.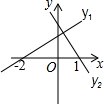 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )| A. | x<-2 | B. | -2<x<1 | C. | x>0 | D. | x>1 |
1.南水北调中线工程向河南、河北、北京、天津四省市供水,通水后每年可向北方输95亿立方米的水量,基本缓解北方严重缺水局面.95亿立方米用科学记数法表示是( )
| A. | 9.5×106m3 | B. | 9.5×107m3 | C. | 9.5×108m3 | D. | 9.5×109m3 |
 如图,在每个小正方形边长为1的网格纸中,将格点△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
如图,在每个小正方形边长为1的网格纸中,将格点△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′. 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).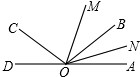 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.
如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.