题目内容
11.一个口袋中装有4个白球、6个红球,这些球除颜色外完全相同,重复搅匀后随机摸出一球,发现是白球.(1)如果将这个白球放回,再摸出一球,那么它是白球的概率是多少?
(2)如果这个白球不放回,再摸出一球,那么它是白球的概率是多少.
分析 (1)摸出一个白球放回对第二次摸到白球没有影响,直接利用概率公式求解即可;
(2)确定摸出一个白球不放回的白球和红球的个数,直接利用概率公式求解即可.
解答 解:(1)如果将白球放回,再摸出一球P(摸到的球是白球)=$\frac{4}{10}$=$\frac{2}{5}$;
(2)如果先摸出一白球,这个白球不放回,那么第二次摸球时,有3个白球和6个红球,再摸出一球P(摸到的球是白球)=$\frac{3}{9}$=$\frac{1}{3}$.
点评 本题考查了概率的公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.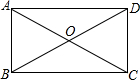 如图,矩形ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AC=8,AB的长度是( )
如图,矩形ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AC=8,AB的长度是( )
 如图,矩形ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AC=8,AB的长度是( )
如图,矩形ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AC=8,AB的长度是( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
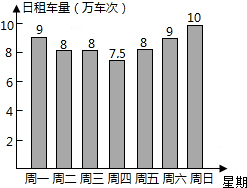 作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车量的统计,结果如图:
作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车量的统计,结果如图: 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.
如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C. 已知一次函数y=ax+b(a,b为常数)经过A(2,0)、B(0,1),求a,b.
已知一次函数y=ax+b(a,b为常数)经过A(2,0)、B(0,1),求a,b.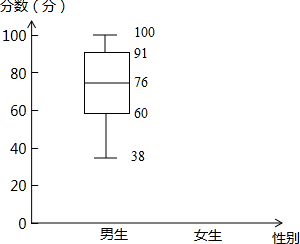 在统计数据时,我们将所有数值由小到大排列并分成四等份,每一部分大约包含25%的数据项,处于三个分割点位置的数从小到大分别记为Q1、Q2、Q3.再将最小值记为M,最大值记为N;
在统计数据时,我们将所有数值由小到大排列并分成四等份,每一部分大约包含25%的数据项,处于三个分割点位置的数从小到大分别记为Q1、Q2、Q3.再将最小值记为M,最大值记为N;